線形最小2乗法(LeastSquareFit)
- Mapleによる最小2乗法
- 最小2乗法の原理
- $\chi^2$の極小値から(2変数の例)
- 正規方程式(Normal Equations)による解
- 特異値分解(Singular Value Decomposition)による解
- 2次元曲面へのフィット
- 課題
Mapleによる最小2乗法
前章では,データに多項式を完全にフィットする補間についてみた.今回は,近似的にフィットする最小二乗法について詳しくみていく.図のようなデータに直線をフィットする場合を考えよう.
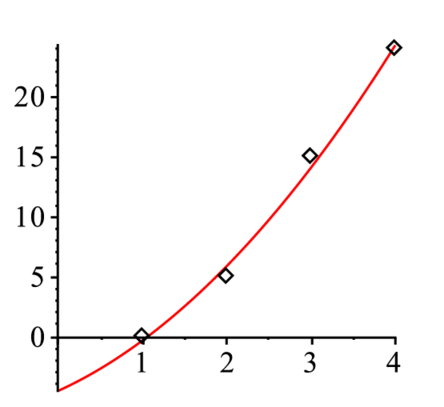 |
コマンドleastsquareによるfitting(2変数の例)
> restart: X:=[1,2,3,4]: Y:=[0,5,15,24]:
> with(plots):with(linalg):with(stats):
> l1:=pointplot(transpose([X,Y]),symbolsize=30):
> eq_fit:=fit[leastsquare[[x, y], y = a0+a1*x, {a0,a1}]]([X, Y]);> f1:=unapply(rhs(eq_fit),x);> p1:=plot(f1(x),x=0..4):
> display(p1,l1);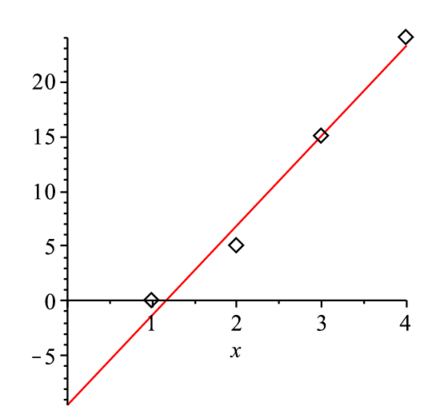 |
最小2乗法の原理
もっとも簡単な例で原理を解説する.近似関数として,
$$ F(x) = a_0+a_1\,x $$という直線近似を考える.もっともらしい関数は$N$点の測定データとの差$d_i = F(x_i)-y_i$を最小にすればよさそうであるが,これはプラスマイナスですぐに消えて不定になる.そこで,
$$ \chi^{2}=\sum_i^N d_i^2=\sum_i^N\left(a_0+a_1\,x_i-y_i\right)^2 $$という関数を考える.この$\chi^2$(カイ二乗)関数が,$a_0, a_1$をパラメータとして変えた時に最小となる$a_0, a_1$を求める.これは,それらの微分がそれぞれ0となる場合である.これは$\chi^2$の和$\sum$(sum)の中身を展開し,
| $\chi^2=$ |
$a_0, a_1$でそれぞれ微分すれば
| $ \frac{\partial}{\partial a_0} \chi^2 =$ | |
| $ \frac{\partial}{\partial a_1} \chi^2 =$ |
という$a_0, a_1$を未知変数とする2元の連立方程式が得られる.これは前に説明した通り逆行列で解くことができる.
$\chi^2$の極小値から(2変数の例)
> restart; X:=[1,2,3,4]: Y:=[0,5,15,24]: f1:=x->a0+a1*x:
S:=0:
for i from 1 to 4 do
S:=S+(f1(X[i])-Y[i])^2;
end do:
> fS:=unapply(S,(a0,a1));> expand(fS(a0,a1));> plot3d(fS(a0,a1),a0=-20..20,a1=0..20);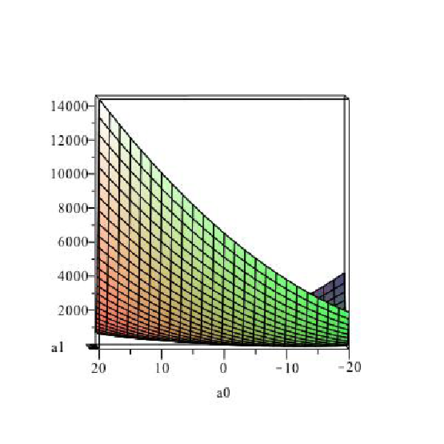 |
> eqs:={diff(expand(S),a0)=0, diff(expand(S),a1)=0};> solve(eqs,{a0,a1});正規方程式(Normal Equations)による解
より一般的な場合の最小二乗法の解法を説明する.先程の例では1次の多項式を近似関数とした.これをより一般的な関数,例えば,$\sin, \cos, \tan, \exp, \sinh$などとする.これを線形につないだ関数を
$$ F \left(x \right)=a _{0}\sin \left(x \right)+a _{1}\cos \left(x \right)+a _{2}\exp \left(-x \right)+a _{3}\sinh \left(x \right)+\cdots ={\sum_{k=1}^{M}}a _{k }X _{k }\left(x \right) $$ととる.実際には,$X_k(x)$はモデルや,多項式の高次項など論拠のある関数列をとる.これらを基底関数(base functions)と呼ぶ.ここで線形といっているのは,パラメータ$a_k$について線形という意味である.このような,より一般的な基底関数を使っても,$\chi^2$関数は
$$ {\chi}^{2}=\sum _{i=1}^{N} \left( F \left( x_{{i}} \right) -y_{{i}} \right) ^{2} =\sum _{i=1}^{N} \left( \sum _{k=1}^{M}a_{{k}}X_{{k}} \left( x_{{i}} \right) -y_{{i}} \right) ^{2} $$と求めることができる.この関数を,$a_k$を変数とする関数とみなす.この関数が最小値を取るのは,$\chi^2$を$M$個の$a_k$で偏微分した式がすべて0となる場合であ る.これを実際に求めてみると,
$$ \sum _{i=1}^{N} \left( \sum _{j=1}^{M}a_{{j}}X_{{j}} \left( x_{{i}} \right) -y_{{i}} \right) X_{{k}} \left( x_{{i}} \right) =0 $$となる.ここで,$k = 1..M$の$M$個の連立方程式である.この連立方程式を最小二乗法の正規方程式(normal equations)と呼ぶ.
上記の記法のままでは,ややこしいので,行列形式で書き直す.$N \times M$で,各要素を
$$ A_{ij} = X_j(x_i) $$とする行列$A$を導入する.この行列は,
$$ A=\left[ \begin{array}{cccc} X_1(x_1) & X_2(x_1) & \cdots & X_M(x_1) \\ \vdots & \vdots & \cdots & \vdots \\ \vdots & \vdots & \cdots & \vdots \\ \vdots & \vdots & \cdots & \vdots \\ X_1(x_N) & X_2(x_N) & \cdots & X_M(x_N) \end{array} \right] $$となる.これをデザイン行列と呼ぶ.すると先程の正規方程式は,
$$ A^t . A . a = A^t . y $$で与えられる.$A^t$は行列$A$の転置(transpose)
$$ A^t = A_{ij}^t = A_{ji} $$を意味し,得られた行列は,$M \times N$である.$a, y$はそれぞれ,
$$ a=\left[ \begin{array}{c} a_1\\a_2\\\vdots\\a_M \end{array} \right],\, y=\left[ \begin{array}{c} y_1\\y_2\\\vdots\\y_N \end{array} \right] $$である.
$M = 3, N = 25$として行列の次元だけで表現すると,
$$ \left[ \begin{array}{ccccc} & & \cdots & &\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ & & \cdots & &\\ \end{array} \right] \left[ \begin{array}{ccc} & \vdots &\\ & \vdots &\\ \cdots & \cdots & \cdots\\ & \vdots &\\ & \vdots &\\ \end{array} \right] \left[ \begin{array}{c} \vdots\\ \vdots\\ \vdots \end{array} \right] = \left[ \begin{array}{ccccc} & & \cdots & &\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ & & \cdots & &\\ \end{array} \right] \left[ \begin{array}{c} \vdots\\ \vdots\\ \vdots\\ \vdots\\ \vdots \end{array} \right] $$となる.これは少しの計算で$3 \times 3$の逆行列を解く問題に変形できる.
Mapleによる具体例
> restart; X:=[1,2,3,4]: Y:=[0,5,15,24]:
f1:=x->a[1]+a[2]*x+a[3]*x^2:
with(LinearAlgebra): Av:=Matrix(1..4,1..3):
ff:=(x,i)->x^(i-1):
for i from 1 to 3 do
for j from 1 to 4 do
Av[j,i]:=ff(X[j],i);
end do;
end do;
Av;> Ai:=MatrixInverse(Transpose(Av).Av);> b:=Transpose(Av).Vector(Y);> Ai.b;特異値分解(Singular Value Decomposition)による解
正規方程式を解くときには,少し注意が必要である.正規方程式での共分散行列,特異値分解の導出や標準偏差との関係はNumRecipeを参照せよ.
> restart; X:=[1,2,3,4]: Y:=[0,5,15,24]: f1:=x->a[1]+a[2]*x+a[3]*x^2:
> with(LinearAlgebra): Av:=Matrix(1..4,1..3):
> ff:=(x,i)->x^(i-1):
for i from 1 to 3 do
for j from 1 to 4 do
Av[j,i]:=ff(X[j],i);
end do;
end do;
Av;> U,S,Vt:=evalf(SingularValues(Av,output=['U','S','Vt'])):
> DiagonalMatrix(S[1..3],4,3); U.DiagonalMatrix(S[1..3],4,3).Vt:> iS:=Vector(3):
for i from 1 to 3 do
iS[i]:=1/S[i];
end do:
> DiS:=DiagonalMatrix(iS[1..3],3,4);> Transpose(Vt).DiS.(Transpose(U).Vector(Y));2次元曲面へのフィット
先程の一般化をより発展させると,3次元$(x_i, y_i, z_i)$で提供されるデータへの,2次元平面でのフィットも可能となる.2次元の単純な曲面は,方程式を使って,
$$ F(x, y) = a_1+a_2\,x+a_3\,y+a_4\,xy+a_5\,x^2+a_6\,y^2 $$となる.デザイン行列の$i$行目の要素は,
$$ [1, x_i, y_i, x_i\,y_i, x_i^2, y_i^2] $$として,それぞれ求める.このデータの変換の様子をMapleスクリプトで詳しく示した.後は,通常の正規方程式を解くようにすれば,このデータを近似する曲面を定めるパラメータ$a_1, a_2, \cdots,a_6$が求まる.最小二乗法はパラメータ$a_k$について線形であればよい.
Mapleによる具体例
実際のデータ解析での例.データの座標をx,y,zで用意して,Mapleの埋め込み関数のleastsquareでfitしている.
> with(plots):with(plottools):
z:=[0.000046079702088, 0.000029479057275,
0.000025769637830, 0.000034951410953, 0.000057024385455, 0.000029485453808,
0.000011519913869, 0.000006442404299, 0.000014252898382, 0.000034951410953,
0.000025769637773, 0.000006442404242, 0.000000000000057, 0.000006442404242,
0.000025769637773, 0.000034932221524, 0.000014246501905, 0.000006442404299,
0.000011519913926, 0.000029479057332, 0.000056973214100, 0.000034932221467,
0.000025769637773, 0.000029485453808, 0.000046079702031]:
> x:=[]:
y:=[]:
p1:=2:
for i from -p1 to p1 do
for j from -p1 to p1 do
x:=[op(x),i*0.0005];
y:=[op(y),j*0.0005];
end do;
end do;
> with(LinearAlgebra): p2:=convert(Transpose(Matrix([x,y,z])),listlist):
pp2:=pointplot3d(p2,symbol=circle,symbolsize=30,color=black):
with(stats): data:=[x,y,z]:
fit1:=fit[leastsquare[[t,s,u],
u=a1+a2*t+a3*s+a4*t*s+a5*t^2+a6*s^2,
{a1,a2,a3,a4,a5,a6}]](data);> f1:=unapply(rhs(fit1),(s,t)):
> pf1:=plot3d(f1(ss,uu),ss=-0.001..0.001,uu=-0.001..0.001,color=gray):
> display(pf1,pp2,axes=boxed);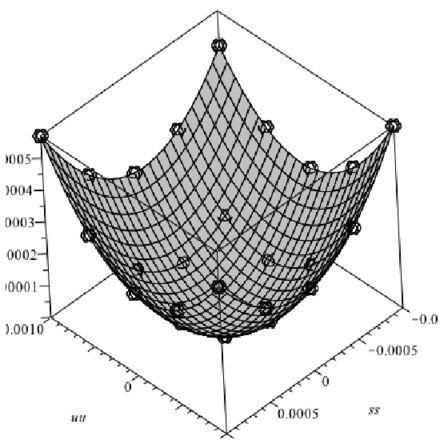 |
正規方程式による解法
デザイン行列へのデータ変換
> bb:=Vector(25): A:=Matrix(25,6):
p1:=2:
for i from 1 to 25 do
A[i,1]:=1;
A[i,2]:=x_i;
A[i,3]:=y_i;
A[i,4]:=x_i*y_i;
A[i,5]:=x_i^2;
A[i,6]:=y_i^2;
bb_i:=z_i;
end do:正規方程式の解
> MatrixInverse(Transpose(A).A).(Transpose(A).bb);課題
- 1次元の線形最小二乗法
次の4点のデータを$y = a_1+a_2 x+a_3 x^2$で近似せよ(2006年度期末試験).
X:=[0,1,2,3];
Y:=[1,3,4,10];- 2次元の最小二乗フィット
以下のデータを
$$ f(x, y) = a_1+a_2 x+a_3 y+a_4 xy $$で近似せよ
x, y, z
-1, -1, 2.00000
-1, 0, 0.50000
-1, 1, -1.00000
0, -1, 0.50000
0, 0, 1.00000
0, 1, 1.50000
1, -1, -1.00000
1, 0, 1.50000
1, 1, 4.00000
Keyword(s):
References:[NumMaple] [NumMapleTOC] [SideMenu]