積分(int)
単純な積分(int)
単純な不定積分.
> int(ln(x),x); #res: x ln(x) - x定積分を実行するには,積分変数の範囲を指定する.
> int(sin(x),x=-Pi..0); #res: -2特異点をもつ場合にも適切に積分結果を求めてくれる.
> int(1/sqrt(x*(2-x)),x=0..2); #res: pi無限区間(infinity)における定積分も同様に計算してくれる.
> int(1/(x^2+4),x=-infinity..infinity); #res: 1/2 pi部分積分法や置換積分法を用いる必要のある複雑な積分も一発で求まる.
> eq:=sqrt(4-x^2);int(eq,x);数学の公式集に載っているような積分も同じコマンドで求まる.
> eq2:=exp(-x^2);int(eq2,x=0..zz);studentパッケージいろいろ
ちょっとぐらい難しい積分も,Mapleは単純にintコマンドだけで実行してくれる.しかし,時には,途中の計算法である部分積分,置換積分,部分分数展開が必要になる.このような計算はstudentパッケージに用意さている.
> with(student):部分積分(integration by parts)
> intparts(Int(x*exp(x),x),x);置換(change of variables)による積分
> Int((cos(x)+1)^3*sin(x), x);
> changevar(cos(x)+1=u, Int((cos(x)+1)^3*sin(x), x=a..b), u);
> changevar(cos(x)+1=u, int((cos(x)+1)^3*sin(x), x), u);部分分数(partial fraction)展開による積分
部分分数(partial fraction)展開による積分では,convertコマンドを用いる.
> pf1:=convert(1/(1+x^3),parfrac,x);
int(pf1,x);- 不定積分:次の不定積分を求めよ.
i) $\int 4\,x+3{dx}$ ,ii)$ \int \frac{1}{ 1+\mbox{e}^{x} }{dx}$ ,iii)$ \int \frac{1}{ \mbox{e}^{-x}+\mbox{e}^{x} }{dx}$ ,iv)$ \int \sqrt{1-{x}^{2}}{dx}$
- 定積分:次の定積分を求めよ.
i)$ \int _{0}^{\pi } \sin x{dx}$ ,ii)$ \int _{0}^{1} \arctan x{dx}$ ,iii)$ \int _{-2}^{2} \frac{1}{ \sqrt{4-{x}^{2}} }{dx}$ ,iv)$ \int _{0}^{1} \frac{1}{ {x}^{2}+x+1 }{dx}$
- (発展課題,重積分)次の2重積分を求めよ.
> int(4*x+3,x);
> int( 1/(1+exp(x)),x);
> int(1/(exp(-x)+exp(x)),x);
> int(sqrt(1-x^2),x);> int(sin(x),x=0..Pi);
> int(arctan(x),x=0..1);
> int(1/(sqrt(4-x^(2))),x=-2..2);
> int(1/(x^2+x+1),x=0..1);> with(plots):
> inequal({x-y>=0,x>=0,x<=1,y>=0},x=-0.5..1.5,y=-0.5..1.5,optionsexcluded=(color=white));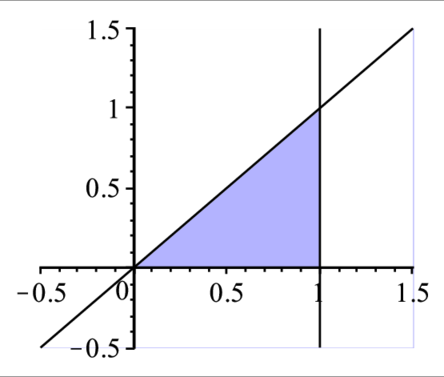 |
> f:=unapply(sqrt(x^2+y^2),(x,y)):
> plot3d(f(x,y),x=0..1,y=0..1,axes=box);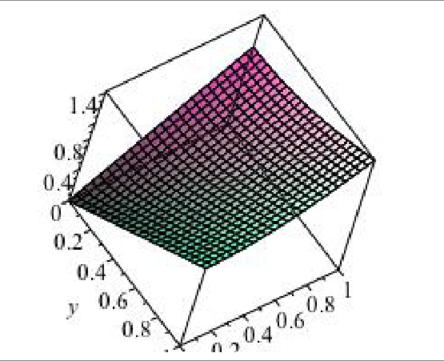 |
> int(int(f(x,y),y=0..x),x=0..1);
Keyword(s):
References:[MaplePrime] [MaplePrimeTOC] [SideMenu]