FFT(Fast Fourier Transformation)
- FFTの応用
- FFTの動作原理
- 関数内挿としてのFourier関数系
- 直交関係からの積分による係数決定
- 直接積分によるフーリエ係数
- 選点直交性による計算の簡素化
- 高速フーリエ変換アルゴリズムによる高速化
- FFT関数を用いた結果
- 課題と解答例
FFT(Fast Fourier Transformation)
FFTの応用
Fast Fourier Transformation(FFT)高速フーリエ変換(あるいはデジタル(離散)フーリエ変換(DFT))は,周波数分解やフィルターを初め,画像処理などの多くの分野で使われている.基本となる考え方は,直交基底による関数の内挿法である.最初にその応用例を見た後,どのような理屈でFFTが動いているかを解説する.
周波数分解
はじめの例は,周波数分解.先ずは,非整合な波を二つ用意しておく.
> restart:
funcs:=[sin(i/13),sin(i/2)];
#funcs:=[sin(i*2),2*sin(i/2)];
plot(funcs,i=0..300);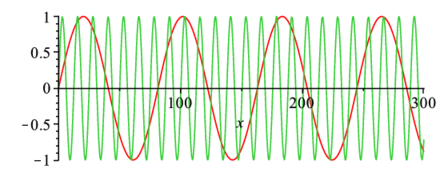 |
これを重ねあわせた波を作る.
> data1:=[]:
for i from 1 to 256 do
data1:=[op(data1),evalf(funcs[1]+funcs[2]))];
end do:
with(plots):
listplot(data1);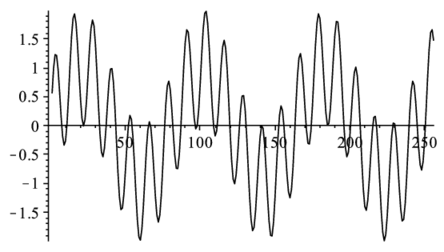 |
ゆっくり変化する波に,激しく変化する波が重なっていることが読み取れる.これにFFTを掛ける
> X:=array(data1):
Y:=array(1..256,sparse):
FFT(8,X,Y);その強さを求めて,周波数で表示すると,
> Data2:=[seq([i,sqrt(X[i]^2+Y[i]^2)],i=1..128)]:
plot(Data2);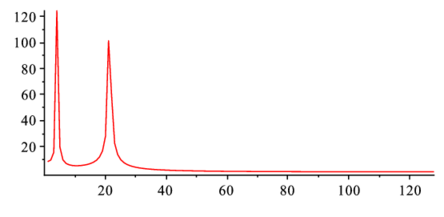 |
もとの2つの周波数に対応するところにピークができているのが確認できる.広がりは,誤差のせい. logplotでも良い.
高周波フィルター
次の例は,高周波フィルター.たとえば次のようなローレンツ関数を考える.
> restart;
f1:=t->subs(a=10,b=40000,c=380,d=128,a+b/(c+(t-d)^2));> plot(f1(t),t=1..256);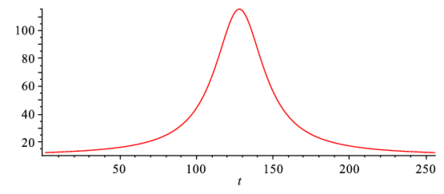 |
これにノイズがのると,次のようになる.
> T:=[seq(f1(i)*(0.6+0.8*evalf(rand()/10^12)),i=1..256)]:
#T:=[seq(evalf(rand()/10^12),i=1..256)]: #これはホワイトノイズ
#T:=[seq(f1(i),i=1..256)]: #これは元の関数そのまま
with(plots):
listplot(T);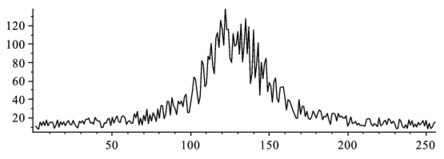 |
これに高周波フィルターを掛けるとノイズが消えるが,その様子を示そう.先ずは,FFTを掛ける.
> Idata:=array([seq(0,i=1..256)]):
Rdata:=convert(T,array):
FFT(8,Rdata,Idata);これは次のような強度分布をもっている.
> Adata:=[seq([i,sqrt(Idata[i]^2+Rdata[i]^2)],i=1..128)]:
> logplot(Adata);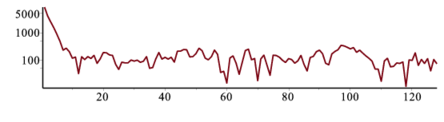 |
低周波の部分に,ゆっくりとした変化を表す成分が固まっている.次のような三角フィルターを用意する.これは,低周波ほど影響を大きくするフィルター.
> filter:=x->piecewise(x>=0 and x<=20,(1-x/20)): #三角フィルター
#filter:=x->piecewise(x>=0 and x<=20,1); #方形フィルター
plot(filter(x),x=0..40);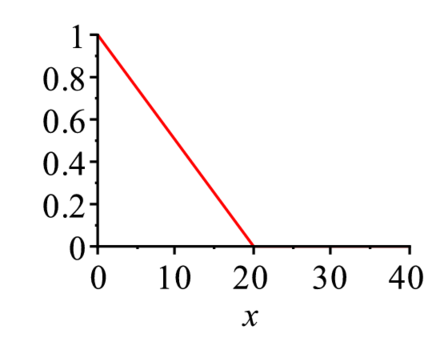 |
これとデータを各点で掛けあわせる事によって,フィルターを通したことになる.
> FRdata:=array([seq(Rdata[i]*filter(i),i=1..256)]):
> FIdata:=array([seq(Idata[i]*filter(i),i=1..256)]):先ほどと同様に表示すると
> Bdata:=[seq([i,sqrt(FIdata[i]^2+FRdata[i]^2)],i=1..128)]:
> logplot(Adata);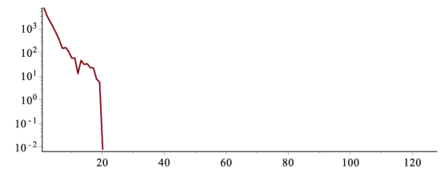 |
$i=20$以上の領域がフィルターによってちょん切られていることが確認できる.これを逆フーリエ変換する.
> iFFT(8,FRdata,FIdata);これを表示すると,
> listplot(FRdata);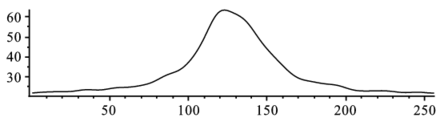 |
となる.ノイズが取り除かれているのが確認できる.元の関数に加えたホワイトノイズにFFTを掛ければ分かるが,全周波数域にわたって均質に広がった関数となる.これを三角フィルターなどで高周波成分をカットすることで,ノイズが取り除かれていくのが理解されよう.
FFTの動作原理
このように便利なFFTであるが,どのような理屈で導かれるのか? Fourier変換法は,この課題だけでも何回ものコマ数が必要なほどの内容を含んでいる.ここでは, その基本となる考え方(のひとつ)だけを提示する.
- 関数の内挿で導入した基底関数を直交関数系でとる.ところが,展開係数を逆行列で求める手法では計算が破綻.
- 直交関係からの積分による係数決定.
- 選点直交性による計算の簡素化.
- 高速フーリエ変換アルゴリズムによる高速化.
関数内挿としてのFourier関数系
一連の関数系による関数の内挿は,基底関数を$\varphi_n(x)$として
$$ F(x) = \sum^N_{n=1}a_n \varphi_n(x) $$で得られることを見た. Fourier変換では基底関数として$\varphi _{n} \left( x \right) =\sin \left( 2\,\pi {\it nx} \right) ,\,\cos \left( 2\,\pi {\it nx} \right)$をとる.関数の内挿法で示したように,この$x_i$での値$f_i, i=1 \cdots M$と,近似の次数($N$)とでつくる係数行列,
$$ A=\left[ \begin{array}{cccc} \varphi_0(x_0)&\varphi_1(x_0)& \cdots &\varphi_N(x_0) \\ \vdots & \vdots & \vdots & \vdots \\ \varphi_0(x_M)&\varphi_1(x_M)& \cdots &\varphi_N(x_M) \end{array}\right] $$を求めて,係数$a_i$とデータ点$f_i$をそれぞれベクトルと考えると,
$$ \boldsymbol{A}.\boldsymbol{a} = \boldsymbol{f} $$から,通常の逆行列を求める手法で係数を決定することもできる.しかし,この強引な方法はデータ数,関数の次数が多い,フーリエ変換が対象としようとする問題では破綻する.もっといい方法が必要で,それが直交関数系では存在する.
直交関係からの積分による係数決定
関数の直交関係は, $$ \int _{a}^{b}\varphi _{n} \left( x \right) \varphi _{m} \left( x \right) {dx}= \delta_{\it mn}C_{n}= \left\{\begin{array}{lr} C_m & at\, n=m \\ 0 & at\, n\neq m \end{array}\right. $$ である.定数$C_m$は,$\sin,\cos$の三角関数系では次の通り.
> plot([sin(x),sin(3*x)],x=0..2*Pi);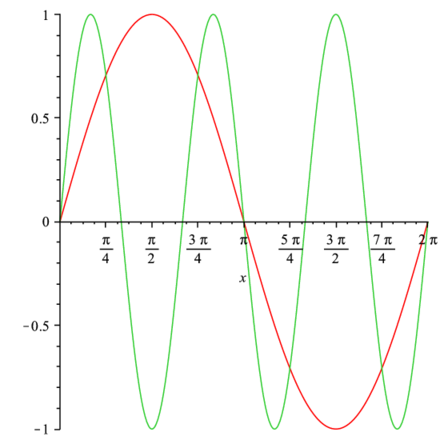 |
> plot([sin(x)*sin(3*x)],x=0..2*Pi, color=black);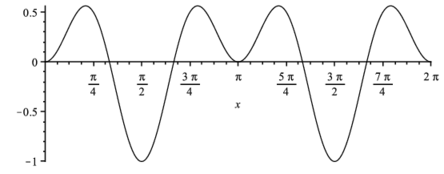 |
> int(sin(x)*sin(3*x),x=0..2*Pi);> for i from 1 to 3 do for j from 1 to 3 do S:=int(sin(i*x)*sin(j*x),x=0..2*Pi);
> print(i,j,S); end do; end do:を考える.先程の\ref{Eq:Orthogonal}式をいれると $$ \int _{a }^{b }F \left(x \right)\varphi _{m }\left(x \right) dx =\int _{a }^{b }{\sum^N_{n=1} }a _{n }\varphi _{n }\left(x \right)\varphi _{m }\left(x \right)d x = \left\{\begin{array}{lr} a_m C_m & at\, n=m \\ 0 & at\, n\neq m \end{array}\right. $$ となる.こうして,係数$a_n$が
$$ a_{{n}}=\frac {1}{C_n}\int _{a}^{b} F \left( x \right) \varphi _{{n}} \left( x \right) {dx} $$で決定できる.
直接積分によるフーリエ係数
対象とする関数をまず作る.
> restart;
> #F:=x->piecewise(x=0,1/2,x>0,x);
#F:=x->piecewise(x<1/2,x,x>=1/2,1-x);
#F:=x->piecewise(x<1/2,-1,x>1/2,1);
F:=x->piecewise(x<1/2,-1,x>=1/2,1);
#F:=x->piecewise(x>0 and x<1/2,-1,x>1/2,1);
#F:=x->x-1/2;
plot(F(x),x=0..1);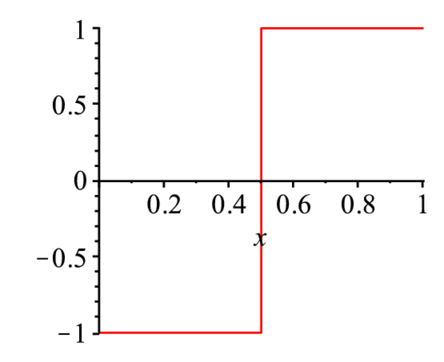 |
piecewise関数は階段関数で,振る舞いはコメント(\#)を適当に外して確認せよ. 初期設定.
> KK:=3; N:=2^KK;L:=1-0;
> 2*Pi*1/L*x;> int(F(x)*cos(2*Pi*1/L*x),x=0..L);> for n from 0 to N do
a[n]:=2/L*int(F(x)*cos(2*Pi*n/L*x),x=0..L);
end do;> for n from 0 to N do
b[n]:=2/L*int(F(x)*sin(2*Pi*n/L*x),x=0..L);
end do;ここで,オイラーの関係 $$ a[n]=c[n]+c[-n],\, b[n]=I (c[n]-c[-n]) \notag \\ c[-n]= \frac{1}{2} (a[n] + b[n]),\, c[n]=\frac{1}{2} (a[n] - I b[n]) $$ を使って,三角関数系から$\exp$へ変換する.
> for n from 0 to N do c[n]:=1/L*int(F(x)*exp(-I*2*Pi*n/L*x),x=0..L); end do;
> for n from 1 to N do c[-n]:=1/L*int(F(x)*exp(I*2*Pi*n/L*x),x=0..L); end do;> F1:=unapply(sum(evalf(c[i]*exp(I*2*Pi*i/L*x)),i=-(N-1)..(N-1)),x):
> plot({Re(F1(x)),F(x)},x=0..1);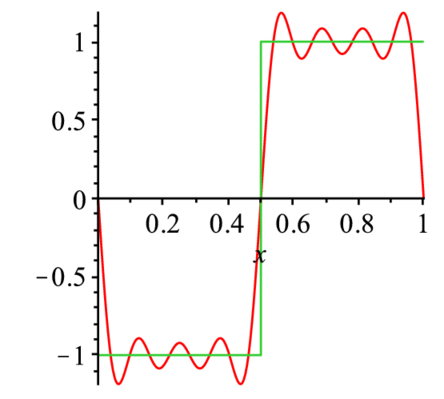 |
> evalf(2/3/Pi);選点直交性による計算の簡素化
ところが,実際に積分していては,時間がかかりすぎる.直交関数系の選点直交性を使うとより簡単になる.
直交関数系の選点直交性
直交多項式は,
$$ \varphi _{n} \left( x \right) =0 \,at\,x_1,\,x_2,\,\cdots x_{n} $$である.$n-1$以下の次数$m,\,l$では,
$$ \sum _{i=1}^{n}\phi_{l} \left( x_{i} \right) \varphi _{m} \left( x_{i} \right) =\delta_{\it ml}C_{l} $$が成り立つ.これは,直交関係と違い積分でないことに注意.証明は略. これを使えば,この先程の直交関数展開
$$ F \left( x \right) =\sum _{l=1}^{N}a_{l}\varphi _{l} \left( x \right) $$の両辺に$\varphi _{m} \left( x_{i} \right)$を掛けて$i$について和をとれば, $$ \sum _{i=1}^{n} F \left(x _{i }\right)\phi _{m }\left(x _{i }\right) = \\ \sum _{i=1}^{n} \sum _{l=1}^{N}a_{l}\varphi _{l} \left( x_{i} \right) \varphi _{m} \left( x_{i} \right) \notag \\ =\sum _{l=1}^{N} a_{l}\sum _{i=1}^{n}\varphi _{l} \left( x_{i} \right) \varphi _{m} \left( x_{i} \right) \notag \\ =\sum _{l=1}^{N}a_{l}\delta_{\it ml}C_{m}=a_{m}C_{m} \notag $$ となる.つまり,
$$ a_{m}=\frac{1}{C_{m}} {\sum _{i=1}^{n}F \left( x_{i} \right) \varphi _{m} \left( x_{i} \right) } $$となり,単純な関数の代入とかけ算で係数が決定される.
選点直交性を用いた結果
> KK:=4; N:=2^KK;L:=1-0;
> for k from 0 to N-1 do
c[k]:=evalf(sum(F(i*L/N)*exp(-I*2*Pi*k*i/N),i=0..N-1));
end do;c_0:=0.
c_1:=-2.000000000 + 10.05467898 I
c_2:=0.
c_3:=-2.000000000 + 2.993211524 I
c_4:=0.
c_5:=-2.000000001 + 1.336357276 I
c_6:=0.
c_7:=-2.000000001 + 0.3978247331 I
c_8:=0.
c_9:=-2.000000001 - 0.3978247331 I
c_10:=0.
c_11:=-2.000000001 - 1.336357276 I
c_12:=0.
c_13:=-2.000000000 - 2.993211524 I
c_14:=0.
c_15:=-2.000000000 - 10.05467898 I> F1:=unapply(sum(evalf(c[i]*exp(I*2*Pi*i/L*x)/N),i=0..(N/2-1))+
> sum(evalf(c[N-i]*exp(-I*2*Pi*i/L*x)/N),i=1..(N/2-1)),x):
> plot({Re(F1(x)),F(x)},x=0..1);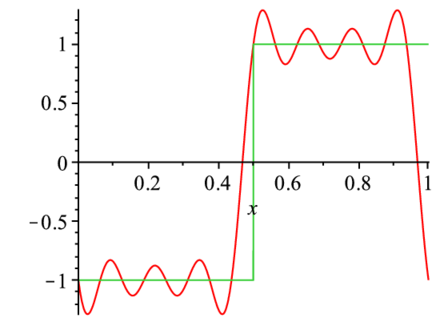 |
高速フーリエ変換アルゴリズムによる高速化
$\sin, \cos$と$\exp$関数を結びつけるオイラーの関係を使うと,
$$ $$と変換できる.これを使うと,
$$ c_{{k}}=\frac{1}{C_{{m}}}\sum _{i=0}^{N-1}F \left( x_{{i}} \right) {{\exp}\left({{\frac {-2\,\pi I}{N}}}\right)} $$となる.$N = 8$の場合を実際に計算すると,$ z = \exp(-\frac{2\pi}{8}I)$として,$z^8=1,z^9=z, \cdots$を使うと,
$$ \left[\begin{array}{c} c_0\\c_1\\c_2\\c_3\\c_4\\c_5\\c_6\\c_7 \end{array}\right] = \left[\begin{array}{cccccccc} 1&1&1&1&1&1&1&1\\ 1&z&z^2&z^3&z^4&z^5&z^6&z^7\\ 1&z^2&z^4&z^6&1&z^2&z^4&z^6\\ 1&z^3&z^6&z&z^4&z^7&z^2&z^5\\ 1&z^4&1&z^4&1&z^4&1&z^4\\ 1&z^5&z^2&z^7&z^4&z^1&z^6&z^3\\ \vdots & & & & & & & \\ \vdots & & & & & & & \end{array}\right] \left[\begin{array}{c} F_0\\F_1\\F_2\\F_3\\F_4\\F_5\\F_6\\F_7 \end{array}\right] $$となる.この行列計算を素直に実行すると,8×8=64回の演算が必要となる.これを減らせないかと考えたのが,高速フーリエ変換の始まりである. この行列をよく見ると同じ計算を重複しておこなっていることが分かる.そこで,行列の左側と右側で同じ計算をしている部分をまとめると,
$$ \left[\begin{array}{c} c_0\\c_1\\c_2\\c_3\\c_4\\c_5\\c_6\\c_7 \end{array}\right] = \left[\begin{array}{cccccccc} 1&1&1&1&0&0&0&0\\ 0&0&0&0&1&z&z^2&z^3\\ 1&z^2&z^4&z^6&0&0&0&0\\ 0&0&0&0&1&z^3&z^6&z\\ 1&z^4&1&z^4&0&0&0&0\\ 0&0&0&0&1&z^5&z^2&z^7\\ 1&z^6&z^4&z^2&0&0&0&0\\ 0&0&0&0&1&z^7&z^6&z^5\\ \end{array}\right] \left[\begin{array}{c} F_0+F_4\\F_1+F_5\\F_2+F_6\\F_3+F_7\\F_0-F_4\\F_1-F_5\\F_{[ \,\,]}-F_6\\F_{[\,\,]}-F_7 \end{array}\right] $$とすることができる.ここで,$z^4 =-1$などを使っている.右側のベクトルの計算でロスするが,行列の中の計算の回数を半分に減らすことができる.再度できあがった行列を見れば,同じ計算をさらにまとめるこ とができそうである.こうして,次々と計算回数を減らしていくことが可能で,最終的に行列部分の計算が一切なくなる.残るのは,右側のベクトルの足し算引き算だけになる.
このベクトルの組み合わせは,一見相当複雑そうで,その条件分岐で時間がかかりそうに思われる.しかし,よく調べてみれば,単純なビット演算で処理することが可能であるこ とが判明した.こうして,2の整数乗のデータの組に対しては,極めて高速にフーリエ変換を実行することが可能となった. FFTでの演算回数は,データ数をNとすると
$$ N\log_2 N $$となる.単純な場合の$N^2$と比較すると,以下のようになり,どれだけ高速化されているかが理解されよう.
> dN2:=[]; dFft:=[]; for i from 2 to 16 do N:=2^i; n2:=N*N; Fft:=N/2*log[2](N);
> Fft/n2; printf("%10d %12d %12d %10.5f\n",N,n2,Fft,evalf(Fft/n2));
> dN2:=[op(dN2),[N,n2]]; dFft:=[op(dFft),[N,Fft]]; end do: 4 16 4 0.25000
8 64 12 0.18750
16 256 32 0.12500
32 1024 80 0.07812
64 4096 192 0.04688
128 16384 448 0.02734
256 65536 1024 0.01562
512 262144 2304 0.00879
1024 1048576 5120 0.00488
2048 4194304 11264 0.00269
4096 16777216 24576 0.00146
8192 67108864 53248 0.00079
16384 268435456 114688 0.00043
32768 1073741824 245760 0.00023
65536 4294967296 524288 0.00012> with(plots):
> l1:=plot(dN2): l2:=plot(dFft):
> display(l1,l2);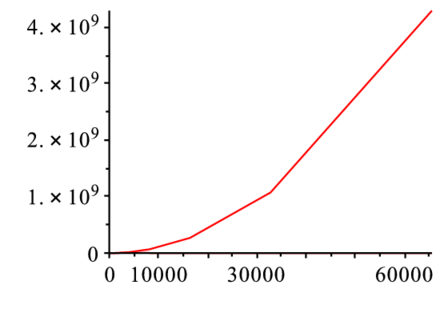 |
> l1:=logplot(dN2): l2:=logplot(dFft):
> display(l1,l2);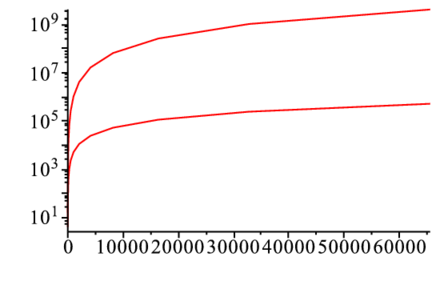 |
> l1:=loglogplot(dN2): l2:=loglogplot(dFft):
> display(l1,l2);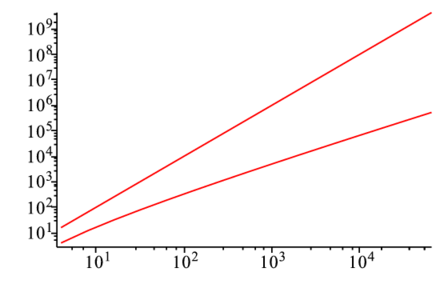 |
FFT関数を用いた結果
> KK:=4;
N:=2^KK;i:='i';L:=1-0;
x1:=array([evalf(seq(F(i/N),i=0..N-1))]);
y1:=array([evalf(seq(0,i=0..N-1))]);> FFT(KK,x1,y1);> interface(displayprecision=2):
print(x1);print(y1);> F2:=unapply(sum(evalf((x1[i]+I*y1[i])*exp(I*2*Pi*(i-1)/L*x)/N),i=1..N/2)+
sum(evalf((x1[N-i+2]+I*y1[N-i+2])*exp(-I*2*Pi*(i-1)/L*x)/N),i=2..N/2),x):
> plot({Re(F2(x)),F(x)},x=0..1);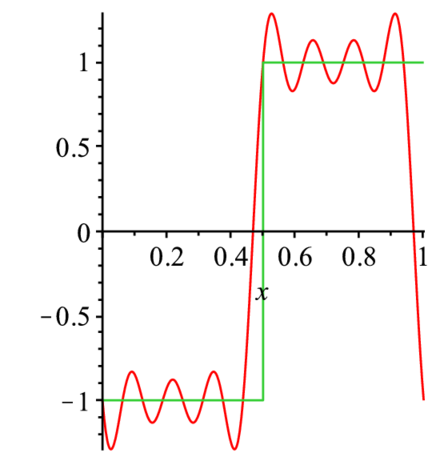 |
課題と解答例
- 課題
下の例に従って,sin(i/13)とsin(i/2)の合成波を作成し,FFTをかけた後,周波数での強度を表示せよ.合成波(2*sin(i*2)+sin(i/2))との違いをのべよ.
- 解答例
restart:
funcs:=[sin(i/13),sin(i/2)];
#funcs:=[2*sin(i*2),sin(i/2)];
plot(funcs,i=0..300);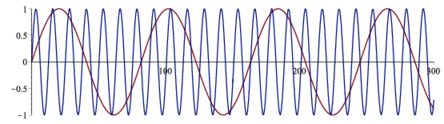 |
> data1:=[]:
for i from 1 to 256 do
data1:=[op(data1),
evalf(funcs[1]+funcs[2])];
# evalf(funcs[1])];
end do:
with(plots):
listplot(data1);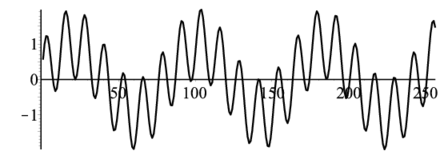 |
> X:=array(data1):
Y:=array(1..256,sparse):
FFT(8,X,Y);> Data2:=[seq([i,sqrt(X[i]^2+Y[i]^2)],i=1..128)]:
plot(Data2);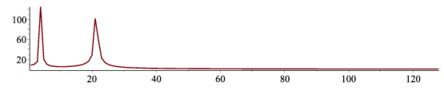 |
Keyword(s):
References:[NumMapleTOC] [SideMenu]