初等関数とそのほかの関数(Functions)

初等関数(ElementaryFunctions)

四則演算とevalf

四則演算は"+-*/"．割り切れない割り算は分数のまま表示される．

> 3/4;

$$ \frac{3}{4} $$

強制的に数値(浮動小数点数)で出力するにはevalfを用いる．

> evalf(3/4);

$$ 0.7500000000 $$

多項式関数(polynom)

かけ算も省略せずに打ち込む必要がある．またベキ乗は\verb="^"=である．

> 3*x^2-4*x+3;

$$ 3x^2-4x+3 $$

平方根(sqrt)

平方根はsquare rootを略したsqrtを使う．

> sqrt(2);

$$ \sqrt{2} $$

三角関数(trigonal)

sin, cosなどの三角関数はラジアンで入力する．ただし， $\sin^2x$などは

> sin^2 x;

Error, missing operator or `;`

ではだめで，

> sin(x)^2;

$$ \sin^2x $$

と省略せずに打ち込まねばならない．三角関数でよく使う定数$\pi$は"Pi"と入力する．Mapleは大文字と小文字を区別するので注意．

ラジアン(radian)に度(degree)から変換するには以下のようにする．

> convert(90*degrees, radians);
  convert(1/6*Pi,degrees);

$$ \frac{1}{2}\pi $$ $$ 30\,\, degrees $$

その他の関数(inifnc)

その他の初等関数やよく使われる超越関数など，Mapleの起動時に用意されている関数のリストは，

> ?inifnc;

で得られる．

ユーザー定義関数(unapply)

初等関数やその他の関数を組み合わせてユーザー定義関数を作ることができる．

関数$f(x) = 2 x - 3$とおくとする場合，Mapleでは，

> f:=x->2*x-3;

$$ f:= x \rightarrow 2 x - 3 $$

と，矢印で書く．これが関数としてちゃんと定義されているかは，いくつかの数値や変数を$f(x)$に代入して確認する．

> f(3);               #res: 3 (以降出力を省略する場合はこのように表記)
  f(a);               #res: 2 a - 3
  plot(f(x),x=-2..2);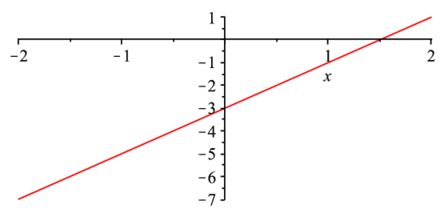

もう一つ関数定義のコマンドとして次のunapplyも同じ意味である．

> f:=unapply(2*x-3,x);

$$ f:= x \rightarrow 2 x - 3 $$

ただし，矢印での定義ではときどき変な振る舞いになるので，unapplyを常に使うようにこころがけたほうが安全．

packageの呼び出し(with)

Mapleが提供する膨大な数の関数から，目的とするものを捜し出すにはhelpを使う．普段は使わない関数は，使う前に明示的に呼び出す必要がある．例えば，線形代数によく使われる関数群は，

> with(LinearAlgebra):

としておく必要がある．この他にもいくつもの有益な関数パッケージが用意されている．

> ?index[package];

で用意されているすべてのpackageが表示される．

関数についての課題

1. evalfのヘルプを参照して，Piを1000桁まで表示せよ．
2. 正接関数(tan)とその逆関数arctanをx=-Pi/2..Pi/2,y=-Pi..Pi,scaling=constrainedで同時にプロットせよ．
3. 対数関数はln(x)で与えられる．ヘルプを参照しながら次の値を求めよ．

$$ \log_{10}1000, \log_{2}\frac{1}{16}, \log_{\sqrt{5}}125 $$

1. 次の関数は$y=2^x$とどのような位置関係にあるかx=-5..5,y=-5..5で同時にプロットして観察せよ．

$$ y = -2^x, y = (1/2)^x,y = -(1/2)^x $$

1. 指数関数はexpで与えられる．$\mbox{e}^x$と$\log x$関数および$y = x$を同時にx=-5..5,y=-5..5でplotせよ．またそれらの関数の位置関係を述べよ．
2. 階乗関数factorialに3を代入して何を求める関数か予測せよ．ヘルプを参照し，よりなじみの深い表記を試してみよ．

Functions

1. evalfのヘルプを参照して，Piを1000桁まで表示せよ．

> ?evalf;
> evalf[1000](Pi);      #省略

1. 正接関数(tan)とその逆関数arctanをx=-Pi/2..Pi/2,y=-Pi..Pi,scaling=constrainedで同時にプロットせよ．

> plot([tan(x),arctan(x)],x=-Pi/2..Pi/2,y=-Pi..Pi,scaling=constrained);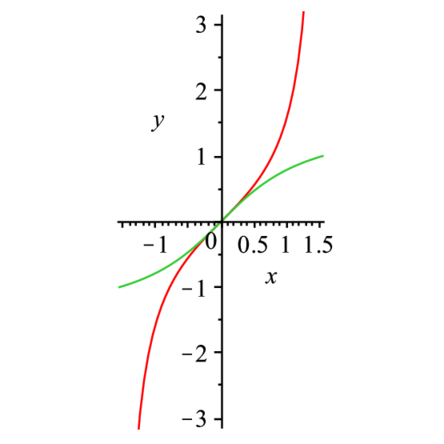

1. 対数関数はln(x)で与えられる．ヘルプを参照しながら次の値を求めよ．

$$ \log_{10}1000, \log_{2}\frac{1}{16}, \log_{\sqrt{5}}125 $$

> ?ln;

> log10(1000);

$$ 3 $$

> log[2](1/16);

$$ -4 $$

> log[sqrt(5)](125);

$$ 6 $$

1. 次の関数は$y=2^x$とどのような位置関係にあるかx=-5..5,y=-5..5で同時にプロットして観察せよ．

$$ y = -2^x, y = (1/2)^x,y = -(1/2)^x $$

> plot([2^x,-2^x,(1/2)^x,-(1/2)^x],x=-5..5,y=-5..5);

注目している関数以外を消せばはっきりするが，i) x軸に対称，ii) y軸に対称, iii) 原点に対称．

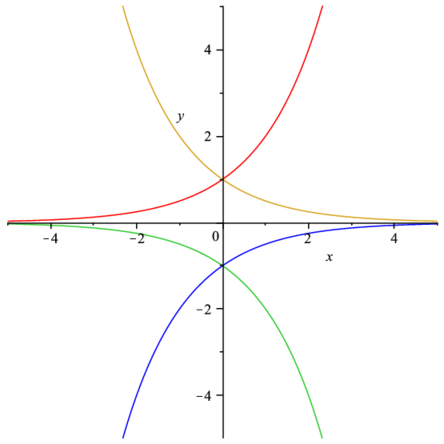1. 指数関数はexpで与えられる．$\mbox{e}^x$と$\log x$関数および$y = x$を同時にx=-5..5,y=-5..5でplotせよ．またそれらの関数の位置関係を述べよ．

> plot([exp(x),log(x),x],x=-5..5,y=-5..5);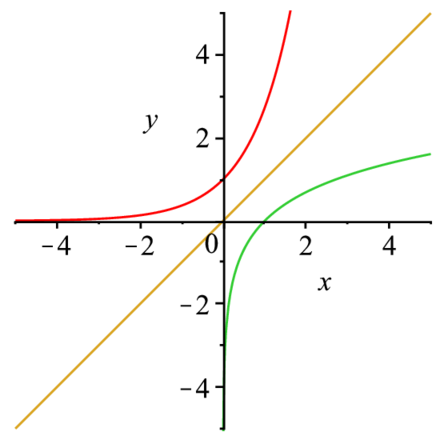

1. 階乗関数factorialに3を代入して何を求める関数か予測せよ．ヘルプを参照し，よりなじみの深い表記を試してみよ．

> factorial(3)

$$ 6 $$

> ?factorial;
> 3!;