Differential(微分)
微積分
微分(Diff)-I
単純な微分(diff)
単純な一変数関数の一次微分は,以下の通り.
> diff(x^2-3*x+2,x); #res: 2x-3高次の微分は,微分変数を必要なだけ並べる.
> diff(sin(x),x,x); #res: -sin(x)さらに高次では次のように\$を使った記法が便利.これはxについての3次微分を表わす.
> diff(x^4,x$3); #res: 24x偏微分(PartialDiff)
複数の変数を持つ多変数の関数では,微分する変数を明示すれば偏微分が求められる.
> eq1:=(x+y)/(x*y);
> diff(eq1,x);例題:関数の微分と増減表
次の関数とその1次導関数を同時にプロットし概形を確認し,さらに増減表を求めよ.
$$ \frac {x}{{x}^{2}-2x+4} $$ !!!!解答例 <<<maple > f0:=unapply(x/(x^2-2*x+4),x): > df:=unapply(diff(f0(x),x),x); > plot([f0(x),df(x)],x); >>> $$ {\it df}\, := \,x\mapsto \left( {x}^{2}-2\,x+4 \right) ^{-1}-{\frac {x \left( 2\,x-2 \right) }{ \left( {x}^{2}-2\,x+4 \right) ^{2}}} $$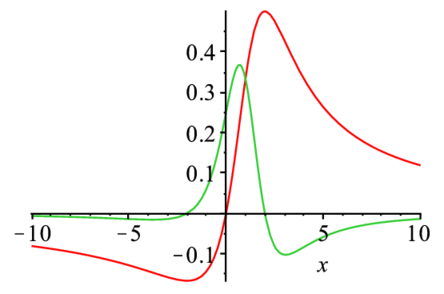 |
例題:接線(Tangent)
次の関数の$ x=3$での接線を求め,2つの関数を同時にプロットせよ.
$$ y={x}^{3}-2\,{x}^{2}-35\,x $$解答例
与関数をf0と定義.
> f0:=unapply(x^3 - 2*x^2 - 35*x,x);微分関数をdfと定義
> df:=unapply(diff(f0(x),x),x);接点(x0,f0(x0))で傾きdf(x0)の直線をf1と定義.
> x0:=3;
> eq1:=df(x0)*(x-x0)+f0(x0);
> f1:=unapply(eq1,x);2つの関数を同時にプロット.
> plot([f0(x),f1(x)],x=-5..5);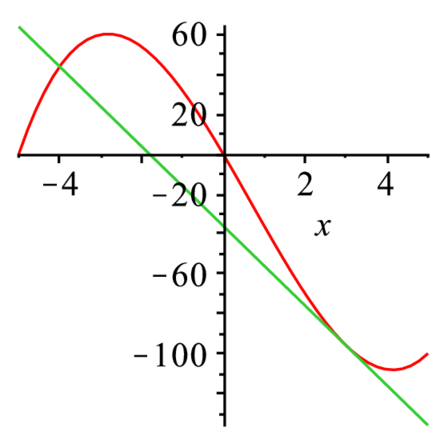 |
微分(Diff)-II
級数展開(series)
Taylor級数は以下のようにして,中心点(x=a),次数(4次)を指定する.
> t1:=series(sin(x),x=a,4);> e1:=convert(t1,polynom);
> f1:=unapply(e1,x);全微分(D)
全微分を計算するときは,Dを用いる.
> f:=unapply(x^4*exp(-y^2),(x,y));
> D(f(x,y));
> (D@@2)(f(x,y));ここで,D(x)などはxの全微分を表わす.これは,x,yを変数としているので
> diff(x,x);
> diff(exp(-y^2),y);であるがMapleには分からない.そこで全微分の最終形を得るには,あらかじめD(x)などの結果を求めておき,subsで明示的に代入する必要がある.
> dd:=D(f(x,y)):
> eqs:={D(x)=diff(x,x),D(exp(-y^2))=diff(exp(-y^2),y)};
> subs(eqs,dd);複合関数の微分
> diff(f(x)*g(x),x);
> diff(f(g(x)),x);> f:=x->exp(x);
> g:=x->cos(x);
> diff(f(x)*g(x),x);
> diff(f(g(x)),x);微分に関する課題
次の関数を微分せよ.
i)$ {x} \log x$, ii) $ \frac{1}{ \left( 1+x \right) ^{3}}$, iii) $ \sqrt{4\,x+3}$, iv) $ \frac{1}{ a^2+ \left( x-x_0 \right)^2 }$
次の関数の1次から5次導関数を求めよ.
i) $\sin^2 x$, ii) ${e}^{x}$
- 以下の関数をx0まわりで3次までテイラー展開し,得られた関数ともとの関数をプロットせよ.さらに5次まで展開した場合はどう変化するか.
i) $ y=\sin x, x_0=0 $, ii) $ y=\cos x, x_0=\frac{\pi}{2}$
(発展課題)$f \left( x,y \right) ={e}^{x}{\it log} \left( 1+y \right) $ を$ x=0,\,y=0$のまわりで3次まで展開せよ.
Diff
> diff(x*log(x),x);
> diff(1/(1 + x)^3,x);
> diff(sqrt(4*x + 3),x);
>diff(1/(a^2+(x-x0)^2),x);> diff(sin(x)^2,x);
> diff(sin(x)^2,x$2);以下略先ず与関数をf0と定義
> f0:=unapply(sin(x),x);テイラー展開した結果をeq1とする.関数として定義するためにeq1を多項式に変換し(convert),unapplyをかける.
> eq1:=series(f0(x),x=0,3);
> f1:=unapply(convert(eq1,polynom),x);5次についても同様
> eq2:=series(f0(x),x=0,5);
> f2:=unapply(convert(eq2,polynom),x);3つの関数を同時プロット
> plot([f0(x),f1(x),f2(x)],x=-Pi..Pi);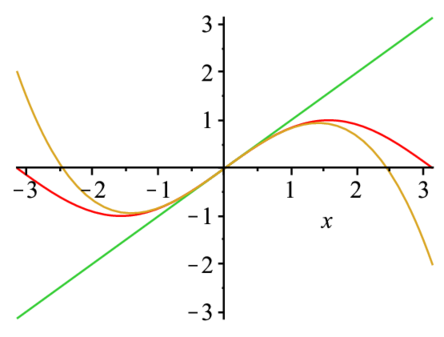 |
> series(f0(x),x=Pi/2,3)以外は前問とおなじ.
f:=unapply(exp(x)*log(1+y),(x,y));eq1:=series(series(f(x,y),x=0,3),y=0,3);> g:=unapply(convert(convert(eq1,polynom),polynom),(x,y));> plot3d([f(x,y),g(x,y)],x=-1..1,y=-1..1,axes=box);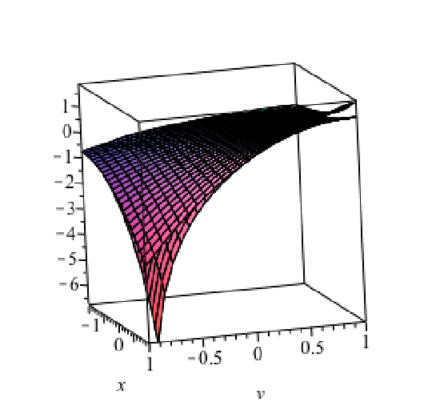 |
きれいな表示
以下のようにすると表示がきれい.
> f:=unapply(x^4*exp(-y^2),(x,y));
> d:=Diff(f(x,y),x);
> d=value(d);
Keyword(s):
References:[MaplePrime] [MaplePrimeTOC] [SideMenu]