“D-ARM” (Discretely-Actuated Robotic Manipulator)
産業界とくに製造現場に向けて様々なメカトロニクス機器が設計製作されています.その中で特にロボット系のアクチュエータには主にACサーボモータが使われています.これは複雑なアプリケーション(例:複雑かつ精緻なアーム手先軌跡制御)においては必須の構成要素ですが,同時にドライバと制御系を含めたコストへの大きな影響が避けられません.しかし比較的シンプルな動作(例:手先指令位置が複数点のみ定められ途中軌跡が重視されない作業)であれば,サーボモータをシステムに組み込まねばならない必然性が失われ,より簡単な構成要素で充分なシステムを構築可能と考えることができます.後者の機器構成論は「最小メカトロニクス系(Minimal mechatronics)」あるいは「素メカトロニクス系(Prime mechatronics)」と呼ばれるシステムの設計問題に帰着します[Erdman, Mason].これは例えば「釣銭計算にスーパーコンピュータは過剰であって電卓で充分」といった一般常識をメカトロニクス系設計へ適用したと理解することもできます[Miller, Goldberg].
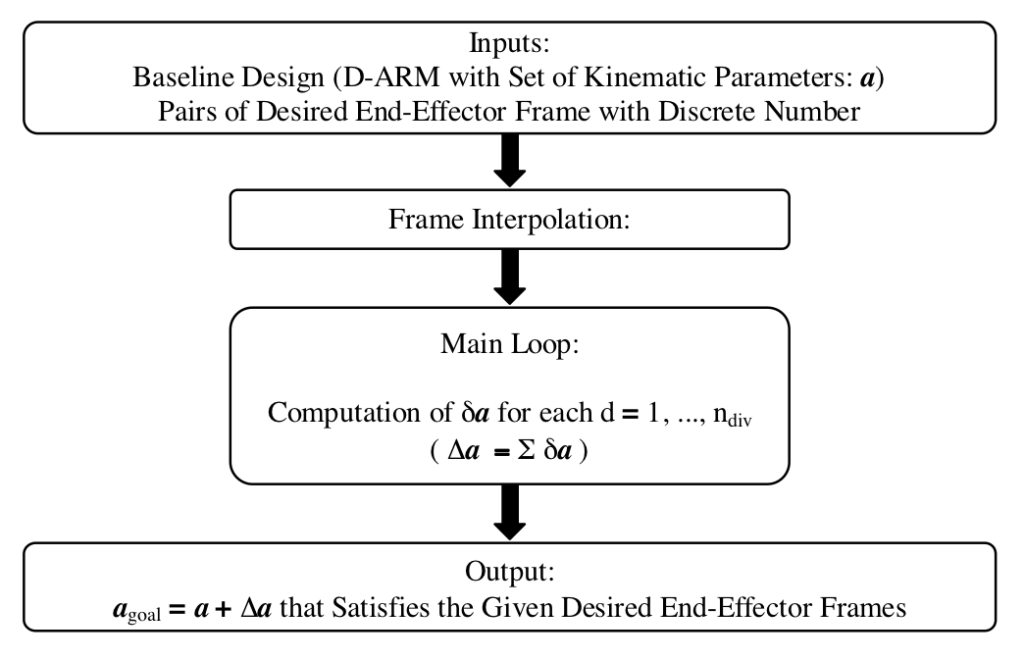
このような考え方に基づくロボットアームの構成法として「離散値駆動型マニピュレータ “D-ARM” (Discretely-Actuated Robotic Manipulator)」が提案されています[Chirikjian, Miyahara].D-ARMは,離散安定点を持つ駆動要素(例:空気圧シリンダ)により構成されるマニピュレータであり「シンプル,安価,高精度(繰返し精度)」という特徴を持っています.本研究の目的は,必要最小限(Necessary minimum)のシステム論を考察することで,メカトロニクス系における資源量対効果の最適化を目指すことにあります.具体的には,与条件である要求性能から,それを満たす「最小システム」を設計する手段を構築することが直近の目標です.
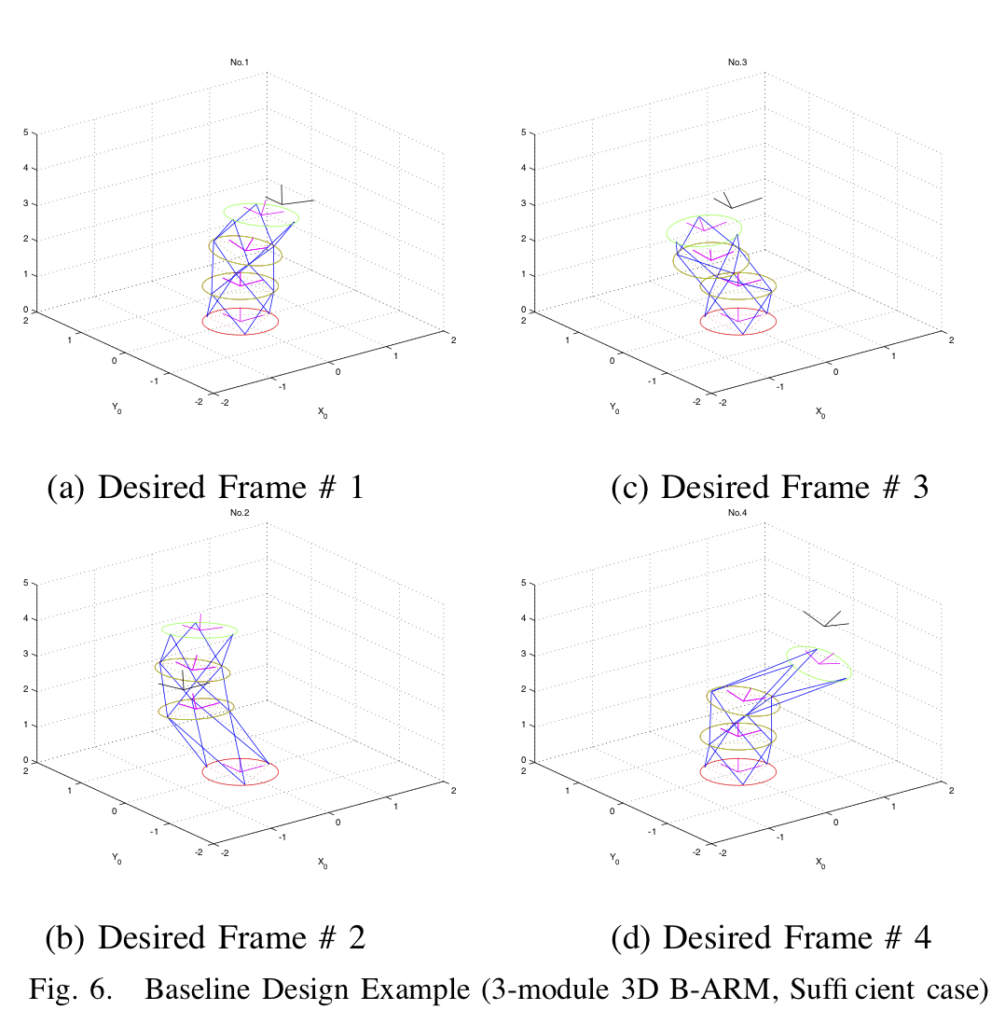
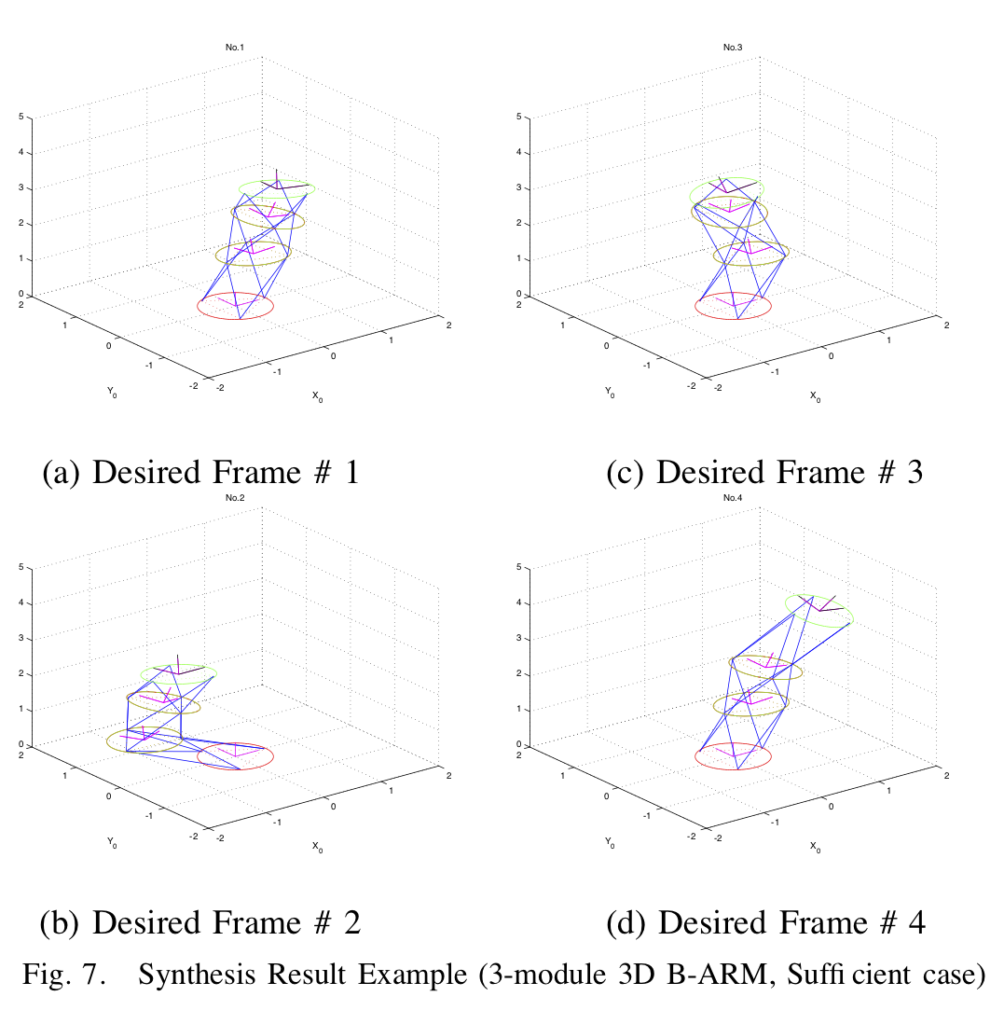
上図は D-ARMの試作機です.離散値駆動されるD-ARMでは手先空間も離散表現されますが,システムを超多自由度(Hyper-redandunt)とすることで離散点が高密度化され,所望手先位置を近似することが可能となります.ただし必要精度に応じて定める自由度の増加に伴って,マニピュレータ動作に関する直感性が急激に失われることに注意が必要です.すなわちD-ARMの実用化を考える場合には,まず順問題(かつ超多自由度問題)として,マニピュレータ形態(configuration)の定式化とその高速計算手法の開発が必要であり,さらに逆問題として,所望手先位置の集合を与条件としてシステムパラメータを求解することができれば「必要最小限のシンプルな機器構成」によって要求動作を達成するシステムが設計可能となります.
これまでに以下のような研究を進めてきました:
D-ARM設計順/逆問題を解決し設計手法を整備
シミュレーションによって実効性を検証
設計プロセス前処理手法を考察
・D-ARM固定座標の最適化手法(設計前誤差の最小化)
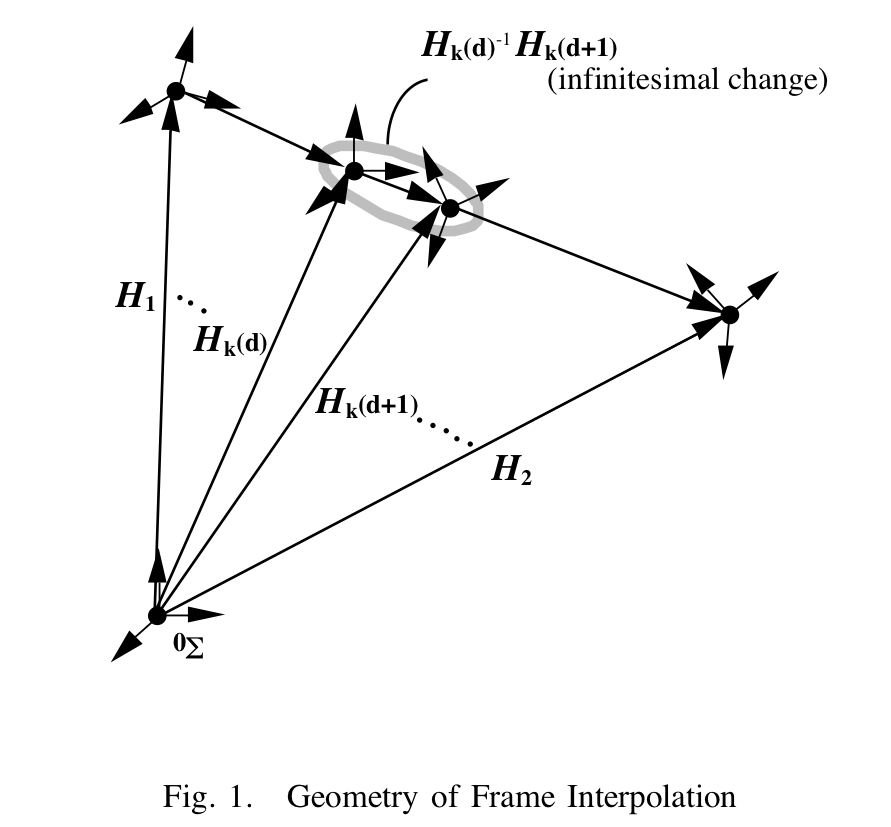
・3次元空間内の任意座標フレーム間の最適分割手法
これらを含む研究成果については Publications をご覧ください.