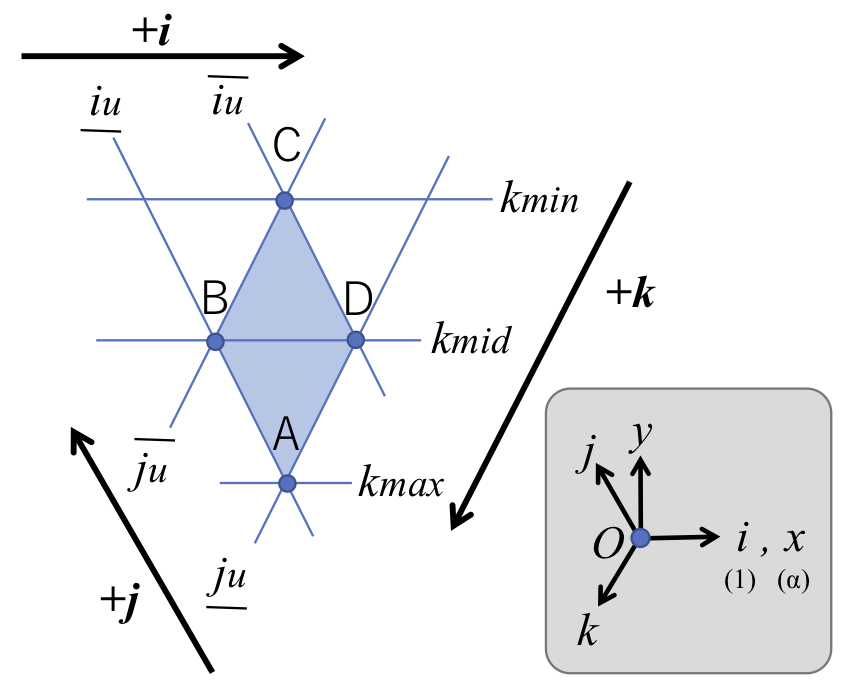
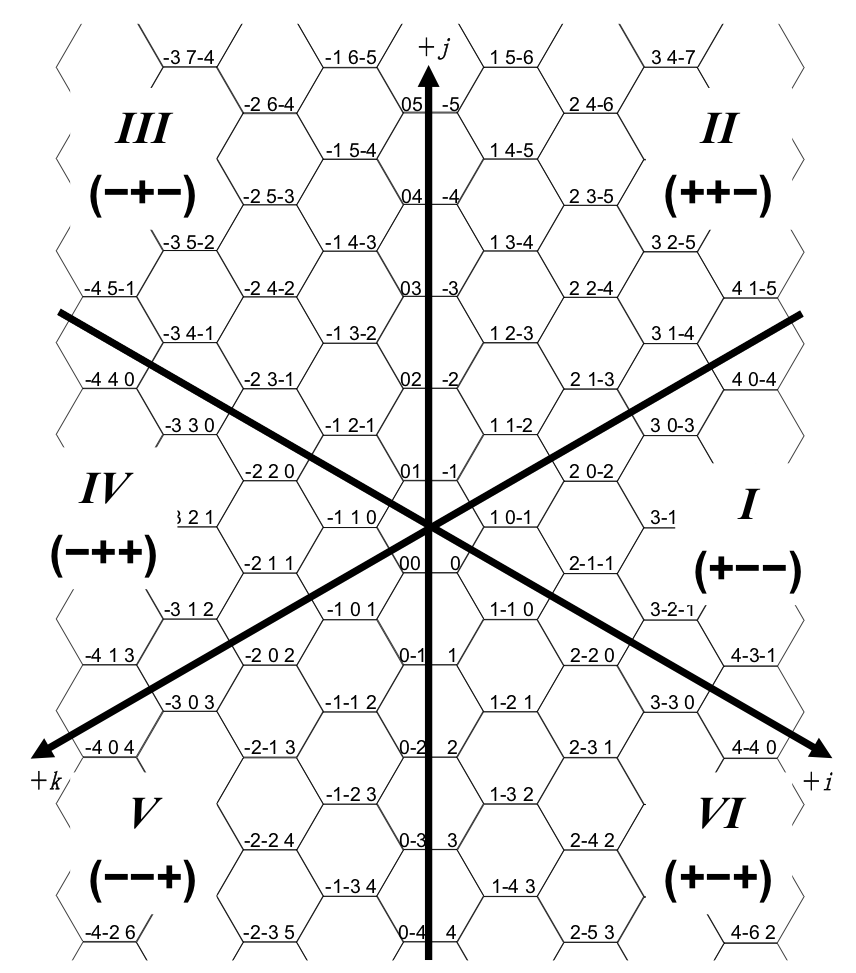
“HCP” (coordinate system for HoneyComb structure by lattice Projection)

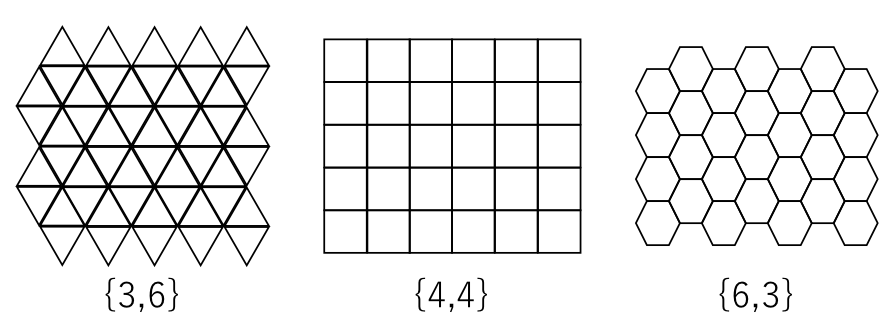
空間を多胞体（Polytopes）により重複なく・隙間なく埋め尽くす構造を「充填」（Tessellation）と呼びます．平面を充填可能な正多角形は，正三角形，正方形，正六角形の3種のみであることが知られています［Pythagoras］．これら3種の「セル」による平面充填は，それぞれ記号を用いて{3,6},{4,4},{6,3}と表されることがあります（各頂点に「p角形」が「q個」集まっている構造を{p,q}と表しています）[Schläfli]．一般に「ハニカム」（Honeycomb）とは{6,3}構造を指す語ですが，より広義に{4,4}や{3,6}構造を含める（さらには全ての平面充填を含める）こともあります．

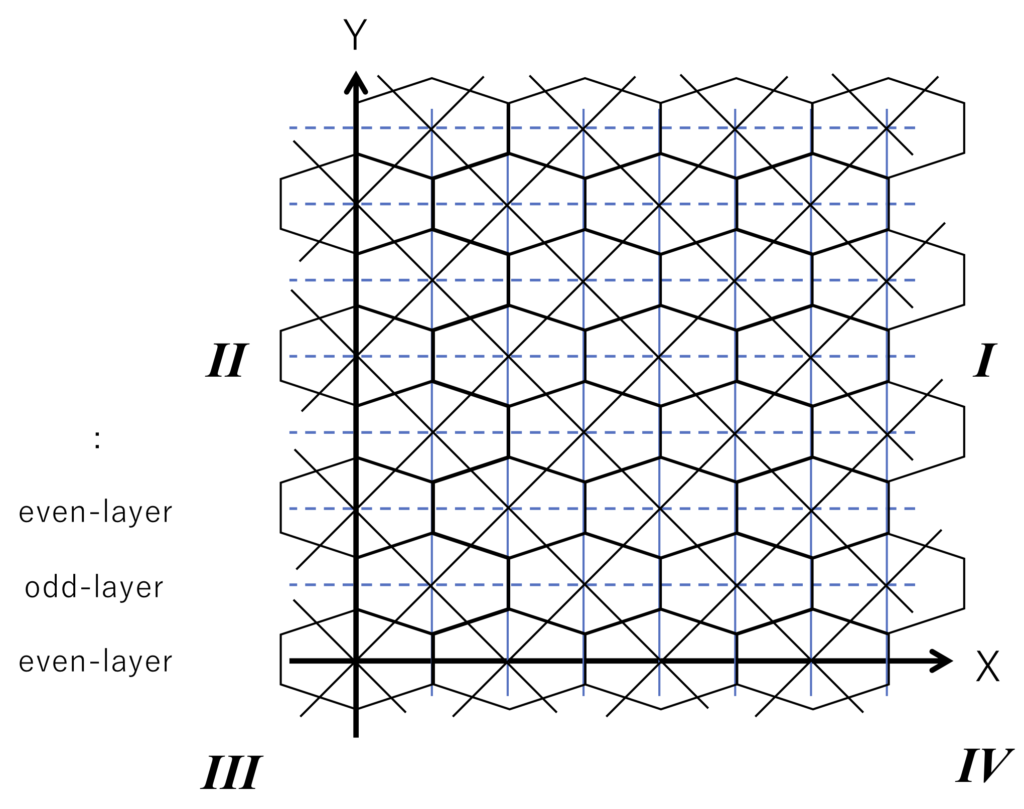
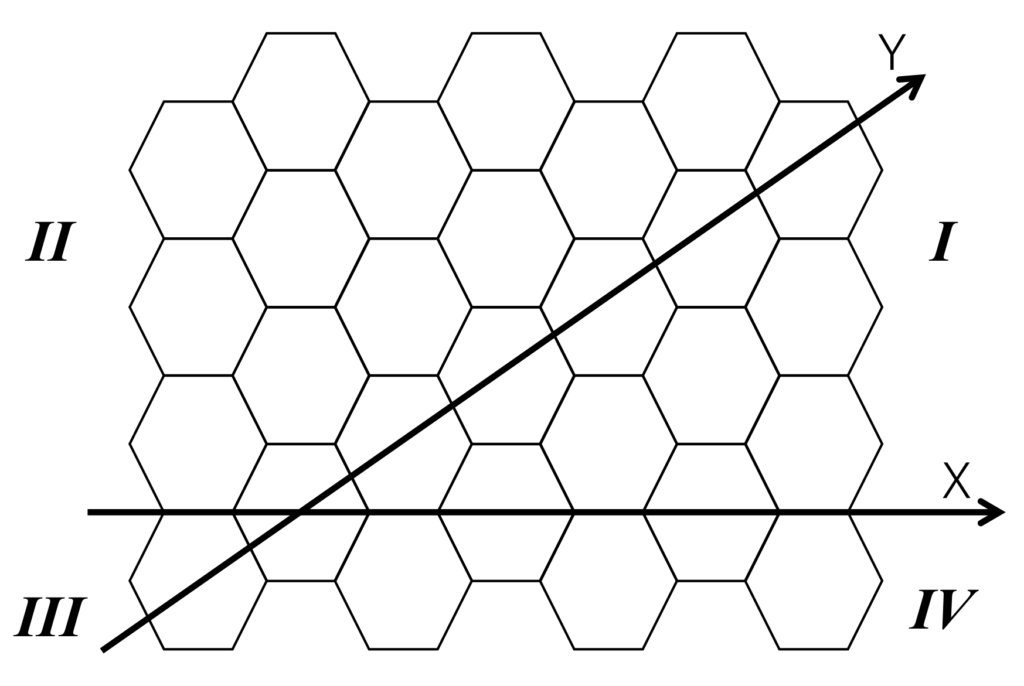
数学的に{4,4}構造を取り扱うためには，直交座標系表現が広く用いられています．しかし直交系は{3,6}あるいは{6,3}構造への親和性が低く，適用時には下図のように，各セルが歪む／座標軸方向のセル密度が異なる等の不都合が生じます．これは，計算機へ実装する際に，特定の座標軸方向での正規化あるいは象限毎の場合分け処理等が不可避であることを示しています．このような不都合は，本質的に3本の対称軸を有する構造へ2軸座標系を無理に適用することが原因であると考えられます．

• 

• 

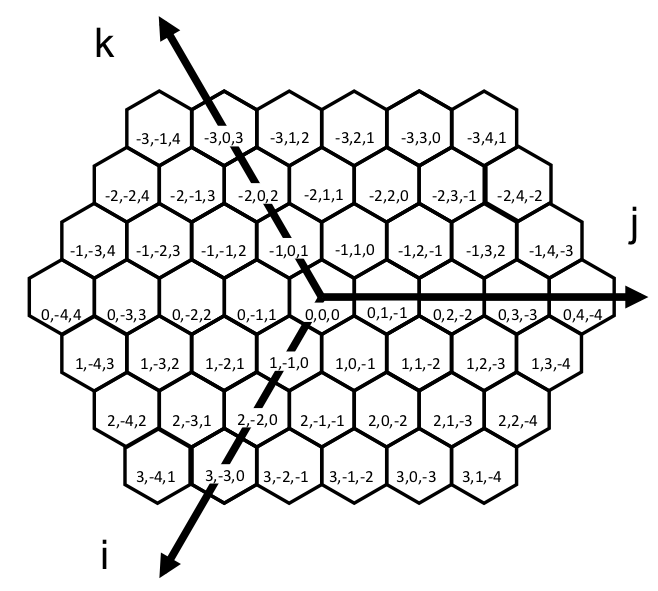
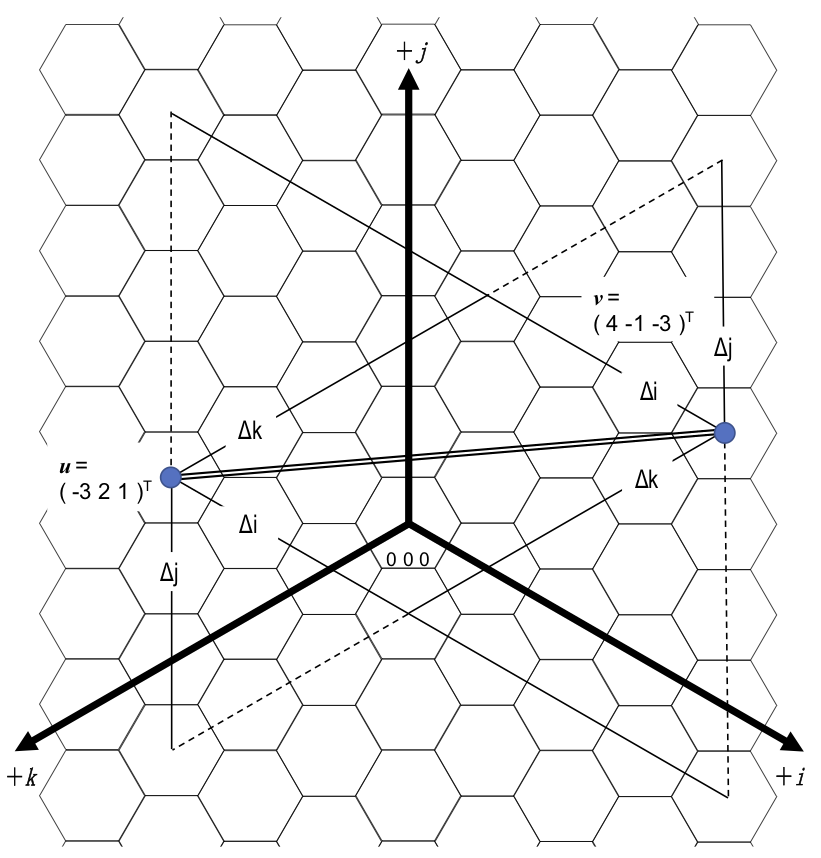
上記の不都合を回避するために，{3,6}および{6,3}構造に適した座標系として“HCP”が提案されています［miyahara］．HCP は3軸から成り，ℤ3 格子（立方体による空間充填）を平面へ射影することにより生成されます．HCP は均質性と等方性，すなわち「セル形状を維持」「軸相対角度が均一」「象限毎のセル配置が均一」という優れた特徴を持っています．
「立方体を平面へ投影してハニカム構造を得る」というアイデアは古くはローマ時代から存在する普遍的なものですが，本研究は，座標系が内包する代数構造を起点に議論を積み重ねており，そのことによって，座標上の演算環境を系統的に考察することが可能となっています．

• 

• 

これまでに以下のような研究を進めてきました：
　座標系の生成手法を詳細に記述
　座標系上の基本的な演算環境を整備
　実問題へ適用しその効果を確認
これらを含む研究成果については Publications をご覧ください．

• 

• 

•