線形代数--固有値(LAEigen)

線形代数--固有値(LAEigen)

$A$を対称正方行列，$x$をベクトルとしたときに， $$ Ax = \lambda x $$ の解，$\lambda$を固有値，$x$を固有ベクトルという．$x$がゼロベクトルではない意味のある解は特性方程式det$(A-\lambda E)=0$が成り立つときにのみ得られる．

まずMapleで特性方程式を解いてみる．

> restart;
> with(LinearAlgebra):with(plots):with(plottools):
> A:=Matrix(1..2,1..2,[[3,2/3],[2/3,2]]);

$$ A\, := \, \left[ \begin {array}{cc} 3&2/3\\2/3&2\end {array} \right] $$

> EE:=Matrix([[1,0],[0,1]]):
  A-lambda.EE;

> eq2:=Determinant(A-lambda.EE);

$$ {\it eq2}\, := \,{\frac {50}{9}}-5\,\lambda+{\lambda}^{2} $$

> solve(eq2=0,lambda);

$$ 10/3,\,5/3 $$

固有値を求めるコマンドEigenvectorsを適用すると，固有値と固有ベクトルが求まる．ここで，固有ベクトルは行列の列(Column)ベクトルに入っている．

> lambda,V:=Eigenvectors(A);

$$ \lambda,\,V\, := \, \left[ \begin {array}{c} 10/3\\5/3\end {array} \right] ,\, \left[ \begin {array}{cc} 2&-1/2\\1&1\end {array} \right] $$

得られた固有ベクトルは規格化されているわけではない．

行列の列を取り出すコマンドColumnを用いて，方程式(\ref{Eq:Eigen})が成り立っていることを確認する．

> lambda[1].Column(V,1)=A.Column(V,1);

$$ \left[ \begin {array}{c} 20/3\\ 10/3\end {array} \right] = \left[ \begin {array}{c} 20/3\\ 10/3\end {array} \right] $$

一般的な規格化は，コマンドNormalize(vector,Euclidean)によっておこなう．

> Normalize(Column(v,1),Euclidean);

次に，固有値の幾何学的な意味を2次元行列で確認しておこう．ある点$x_0$に対称正方行列$A$を作用すると，$x_1$に移動する．これを原点を中心とする円上の点に次々に作用させ，移動前後の点を結ぶ．

> restart;
  with(LinearAlgebra):with(plots):with(plottools):
  A:=Matrix(1..2,1..2,[[3,2/3],[2/3,2]]):

> N:=30:p1:=[]:l1:=[]:
for k from 0 to N-1 do
  x0:=Vector([sin(2*Pi*k/N),cos(2*Pi*k/N)]);
  x1:=MatrixVectorMultiply(A,x0);
  p1:=[op(p1),pointplot({x0,x1})];
  l1:=[op(l1),line( evalf(convert(x0,list)),evalf(convert(x1,list)) )];
end do:

> n:=4;
  display(p1,l1,view=[-n..n,-n..n]);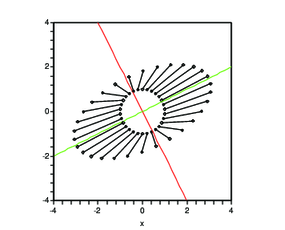

真ん中の円状の領域が，外側の楕円状の領域に写像されている様子が示されている．この図の中に固有ベクトル，固有値が隠れている．どこかわかる？

多くの良質なページからリンクされているページはやはり良質なページである

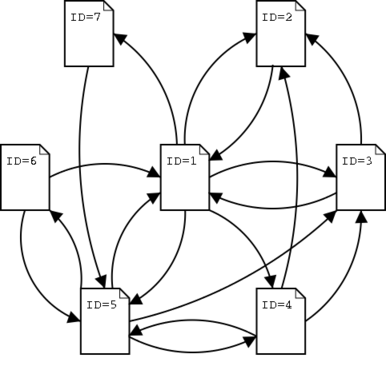
Googleのpage rankは上のような非常に単純な仮定から成り立っている．ページランクを実際に求めよう．つぎのようなリンクが張られたページを考える．

計算手順は以下の通り\footnote{詳しくは\texttt{http://www.kusastro.kyoto-u.ac.jp/\~baba/wais/pagerank.html}を参照せよ．}．

1. リンクを再現する隣接行列を作る．ページに番号をつけて，その間が結ばれているi-j要素を1，そうでない要素を0とする．
2. 隣接行列を転置する
3. 列ベクトルの総和が1となるように規格化する．
4. こうして得られた推移確率行列の最大固有値に属する固有ベクトルを求め，適当に規格化する．

課題

1. 上記手順を参考にして，Mapleでページランクを求めよ．
2. このような問題ではすべての固有値・固有ベクトルを求める必要はなく，最大の固有値を示す固有ベクトルを求めるだけでよい．初期ベクトルを適当に決めて，何度も推移確率行列を掛ける反復法でページランクを求めよ．

隣接行列

$$ {\it A1}\, := \, \left[ \begin {array}{c|c|c|c|c|c|c|c} &1&2&3&4&5&6&7\\ 1&0&1&1&1&1&0&1\\ 2&1&0&0&0&0&0&0\\ 3& & & & & & & \\ 4& & & & & & & \\ 5& & & & & & & \\ 6& & & & & & & \\ 7& & & & & & & \end {array} \right] $$

転置行列

$$ {Transpose}({\it A1})\, := \, \left[ \begin {array}{c|c|c|c|c|c|c} \, \, &\, \, &\, \, &\, \, &\, \, &\, \, &\, \, \\ & & & & & & \\ & & & & & & \\ & & & & & & \\ & & & & & & \\ & & & & & & \\ & & & & & & \end {array} \right] $$

規格化

$$ \left[ \begin {array}{c|c|c|c|c|c|c} \, \, &\, \, &\, \, &\, \, &\, \, &\, \, &\, \, \\ & & & & & & \\ & & & & & & \\ & & & & & & \\ & & & & & & \\ & & & & & & \\ & & & & & & \end {array} \right] $$

遷移

$$ \left( \begin {array}{ccccccc} 0 &1 &1/2 &0 &1/4 &1/2 &0 \\ 1/5 &0 &1/2 &1/3 &0 &0 &0 \\ 1/5 &0 &0 &1/3 &1/4 &0 &0 \\ 1/5 &0 &0 &0 &1/4 &0 &0 \\ 1/5 &0 &0 &1/3 &0 &1/2 &1 \\ 0 &0 &0 &0 &1/4 &0 &0 \\ 1/5 &0 &0 &0 &0 &0 &0 \end {array} \right) \left( \begin {array}{c} 1/7\\ 1/7\\ 1/7\\ 1/7\\ 1/7\\ 1/7\\ 1/7 \end {array} \right) \, = \, \left( \begin {array}{ccccccc} \, \, &\, \, &\, \, &\, \, &\, \, &\, \, &\, \, \\ & & & & & & \\ & & & & & & \\ & & & & & & \\ & & & & & & \\ & & & & & & \\ & & & & & & \end {array} \right) \, = \, \left( \begin {array}{c} 0.32\\ 0.15\\ 0.11\\ 0.06\\ 0.29\\ 0.04\\ 0.03 \end {array} \right) $$

累乗(べき乗)法は，最大固有値とその固有ベクトルを効率的に見つける算法である．すこし，固有値について復習しておく．正方行列$A$に対して， $$ A x = \lambda x $$ の解$\lambda$を固有値，$x$を固有ベクトルという．$\lambda$は， $$ \det( A - \lambda E) =0 $$ として求まる永年方程式の解である．

では，なぜ適当な初期ベクトル$x_0$から始めて，反復 $$ x_{k+1} = A x_k $$ を繰り返すと，$A$の絶対値最大の固有値に属する固有ベクトルに近づいていくのかを見ておこう．

すべての固有値がお互いに異なる場合を考える．今，行列の固有値を絶対値の大きなもの順に並べて，$|\lambda_1|>|\lambda_2|>\cdots>|\lambda_n|$とし，対応する長さを1に規格化した固有ベクトルを$x_1, x_2, \ldots, x_n$とする．初期ベクトルは固有ベクトルの線形結合で表わせて， $$ X_0 = c_1x_1+c_2x_2+\cdots+c_nx_n $$ となるとする．これに行列$A$を$N$回掛けると， $$ A^N X_0 = c_1 \lambda_1^N x_1+ c_2 \lambda_2^N x_2+\cdots+ c_n \lambda_n^N x_n $$ となる．これを変形すると， $$ A^NX_0 = X_{N} = c_1 \lambda_1^N \left\{ x_1+ \frac{c_2}{c_1}\left(\frac{\lambda_2}{\lambda_1}\right)^N x_2+\cdots+ \frac{c_n}{c_1}\left(\frac{\lambda_n}{\lambda_1}\right)^N x_n \right\} $$ となる．$|\lambda_1|>|\lambda_i|(i\ge2)$だから括弧の中は$x_1$だけが生き残る．

こうして最大固有値に属する固有ベクトルが，反復計算を繰り返すだけで求められる．

固有値を求める手法として，永年方程式を解くというやり方は回りくどすぎる．少し古めかしいが非対角要素を0にする回転行列を反復的に作用させるJacobi(ヤコビ)法を紹介する．現在認められている最適の方策は，ハウスホルダー(Householder)変換で行列を単純な三重対角化行列に変形してから，反復法で解を追い込んでいくやり方である．Jacobi法は，Householder法ほど万能ではないが，10次程度までの行列には今でも役に立つ．

Mapleでみる回転行列

行列の軸回転の復習をする．対称行列$B$に回転行列$U$を作用すると $$ B.U = \left( \begin{array}{cc} {a_{1\,1}} & {a_{1\,2}}\\ {a_{2\,1}(={a_{1\,2}})} & {a_{2\,2}} \end{array} \right) \left( \begin{array}{cc} \cos(\theta) & -\sin(\theta)\\ \sin(\theta) & \cos(\theta) \end{array} \right) $$

となる．回転行列を4x4の行列に $$ U^t B U $$ と作用させたときの各要素の様子を以下に示した．

> restart:
> n:=4:
> with(LinearAlgebra):
> B:=Matrix(n,n,shape=symmetric,symbol=a);

$$ B := \left[{ \begin{array}{cccc} {a_{1, \,1}} & {a_{1, \,2}} & {a_{1, \,3}} & {a_{1, \,4}} \\ {a_{1, \,2}} & {a_{2, \,2}} & {a_{2, \,3}} & {a_{2, \,4}} \\ {a_{1, \,3}} & {a_{2, \,3}} & {a_{3, \,3}} & {a_{3, \,4}} \\ {a_{1, \,4}} & {a_{2, \,4}} & {a_{3, \,4}} & {a_{4, \,4}} \end{array}} \right] $$

> U:=Matrix(n,n,[[c,-s,0,0],[s,c,0,0],[0,0,1,0],[0,0,0,1]]);
#U:=Matrix(n,n,[[c,-s],[s,c]]);

$$ U := \left[ {\begin{array}{ccrr} c & - s & 0 & 0 \\ s & c & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}} \right] $$

>TT:=Transpose(U).B.U;

$$ \mathit{TT} := \\ \notag {\begin{array}{c} \left[ \right. (c\,{a_{1, \,1}} + s\,{a_{1, \,2}})\,c + (c\,{a_{1, \,2}} + s \,{a_{2, \,2}})\,s\,, \, - (c\,{a_{1, \,1}} + s\,{a_{1, \,2}})\,s + (c\,{a_{1, \,2}} + s\,{a_{2, \,2}})\,c\,, \\ c\,{a_{1, \,3}} + s\,{a_{2, \,3}}\,, \,c\,{a_{1, \,4}} + s\,{a_{2 , \,4}} \left. \right] \\ \left[ \right. ( - s\,{a_{1, \,1}} + c\,{a_{1, \,2}})\,c + ( - s\,{a_{1, \,2 }} + c\,{a_{2, \,2}})\,s\,, \, - ( - s\,{a_{1, \,1}} + c\,{a_{1, \,2}})\,s + ( - s\,{a_{1, \,2}} + c\,{a_{2, \,2}})\,c\,, \\ - s\,{a_{1, \,3}} + c\,{a_{2, \,3}}\,, \, - s\,{a_{1, \,4}} + c \,{a_{2, \,4}} \left. \right] \\ \left[ c\,{a_{1, \,3}} + s\,{a_{2, \,3}}\,, \, - s\,{a_{1, \,3}} + c\,{a_{2, \,3}}\,, \,{a_{3, \,3}}\,, \,{a_{3, \,4}} \right] \\ \left[ c\,{a_{1, \,4}} + s\,{a_{2, \,4}}\,, \, - s\,{a_{1, \,4}} + c\,{a_{2, \,4}}\,, \,{a_{3, \,4}}\,, \,{a_{4, \,4}} \right] \end{array}} $$

>expand(TT[1,1]);
expand(TT[2,2]);
expand(TT[1,2]);
expand(TT[2,1]);

$$ c^{2}\,{a_{1, \,1}} + 2\,c\,s\,{a_{1, \,2}} + s^{2}\,{a_{2, \,2}} $$ $$ s^{2}\,{a_{1, \,1}} - 2\,c\,s\,{a_{1, \,2}} + c^{2}\,{a_{2, \,2}} $$ $$ - s\,c\,{a_{1, \,1}} - s^{2}\,{a_{1, \,2}} + c^{2}\,{a_{1, \,2}} + c\,s\,{a_{2, \,2}} $$ $$ - s\,c\,{a_{1, \,1}} - s^{2}\,{a_{1, \,2}} + c^{2}\,{a_{1, \,2}} + c\,s\,{a_{2, \,2}} $$

この非対角要素を0にする$\theta$は以下のように求まる．

このとき注目している$i,j=1,2$以外の要素も変化する．

>expand(TT[3,1]);
expand(TT[3,2]);

$$ c\,{a_{1, \,3}} + s\,{a_{2, \,3}} $$ $$ - s\,{a_{1, \,3}} + c\,{a_{2, \,3}} $$

これによって一旦0になった要素も値を持つが，なんども繰り返すことによって，徐々に0へ近づいていく．

以下にはヤコビ法を用いた固有値と固有ベクトルを求めるコードを示した．結果は，固有値とそれに対応する規格化された固有ベクトルが縦(column)ベクトルで表示される．

リスト: ヤコビ法．

#include <stdio.h>
#include <math.h>

#define M 10
void PrintMatrix(double a[M][M], int n);

int main(void){
  double a[M][M],v[M][M];
  double eps=0.0001,div,r,t,s,c,apj,aqj,aip,aiq,vip,viq;
  int i,j,n,iter,count,iterMax=1000000,p,q;
  
  scanf("%d",&n);
  for(i=1;i<=n;i++){
    for(j=1;j<=n;j++) scanf("%lf",&a[i][j]);
  }
  PrintMatrix(a,n);
  for(i=1;i<=n;i++){
    for(j=1;j<=n;j++) v[i][j]=0.;    
    v[i][i]=1.;
  }
  
  for(iter=1;iter<=iterMax;iter++){
    count=0;
    for(p=1;p<=n-1;p++){
      for(q=p+1;q<=n;q++){
	if(fabs(a[p][q])<eps) continue;
	count++;
	div=a[p][p]-a[q][q];
	if (div != 0.0){
	  r=2.0*a[p][q]/div;
	  t=0.5*atan(r);
	} else {
	  t=0.78539818;
	}
	s=sin(t);
	c=cos(t);
	for(j=1;j<=n;j++){
	  apj=a[p][j];
	  aqj=a[q][j];
	  a[p][j]=apj*c+aqj*s;
	  a[q][j]=-apj*s+aqj*c;
	}
	for(i=1;i<=n;i++){
	  aip=a[i][p];
	  aiq=a[i][q];
	  a[i][p]=aip*c+aiq*s;
	  a[i][q]=-aip*s+aiq*c;
	  vip=v[i][p];
	  viq=v[i][q];
	  v[i][p]=vip*c+viq*s;
	  v[i][q]=-vip*s+viq*c;
	}
	printf("p,q=%3d,%3d\n",p,q);
	PrintMatrix(a,n);
      }
    }
    if (count==0) break;
  }
  printf("Eigen values:\n");
  for(i=1;i<=n;i++) printf("%6.2f",a[i][i]);
  printf("\nEigen vectors:\n");
  PrintMatrix(v,n);
  
  return 0;
}

void PrintMatrix(double a[M][M], int n){
  int i,j;
  for(i=1;i<=n;i++){
    for(j=1;j<=n;j++) printf("%6.2f",a[i][j]);
    printf("\n");
  }
  printf("\n");
}

リスト: ヤコビ法の計算結果．

[BobsNewPBG4:~/NumRecipe/chap8] bob% cat input.txt
4
5 4 1 1
4 5 1 1
1 1 4 2
1 1 2 4

BobsNewPBG4:~/NumRecipe/chap8] bob% Jacobi2<input.txt
  5.00  4.00  1.00  1.00
  4.00  5.00  1.00  1.00
  1.00  1.00  4.00  2.00
  1.00  1.00  2.00  4.00

p,q=  1,  2
  9.00 -0.00  1.41  1.41
 -0.00  1.00 -0.00 -0.00
  1.41 -0.00  4.00  2.00
  1.41 -0.00  2.00  4.00

p,q=  1,  3
  9.37 -0.00 -0.00  1.88
 -0.00  1.00  0.00 -0.00
 -0.00  0.00  3.63  1.57
  1.88 -0.00  1.57  4.00

p,q=  1,  4
  9.96 -0.00  0.47 -0.00
 -0.00  1.00  0.00  0.00
  0.47  0.00  3.63  1.50
  0.00  0.00  1.50  3.41

...<中略>...

Eigen values:
 10.00  1.00  5.00  2.00
Eigen vectors:
  0.63 -0.71 -0.32  0.00
  0.63  0.71 -0.32  0.00
  0.32  0.00  0.63 -0.71
  0.32  0.00  0.63  0.71

一般の数値計算ライブラリーについては，時間の関係で講義ではその能力を紹介するにとどめる．昔の演習で詳しく取り上げていたので，研究や今後のために必要と思うときは，テキストを取りにおいで．

行列の計算は，数値計算の中でも特に利用する機会が多く，また，律速ルーチンとなる可能性が高い．そこで，古くから行列計算の高速ルーチンが開発されてきた．なかでもBLASとLAPACKはフリーながら非常に高速である．

前回に示した，逆行列を求める単純なLU分解法をC言語でコーディングしたものと，LAPACKのルーチンを比べた場合，1000次元の行列で計測すると

>  1000 [dim]     2.5200 [sec] #BOB
>  1000 [dim]     0.4700 [sec] #LAPACK

となった．2006年に初めてこの計算に用いたPCはMacBook(2GHz, Intel Core Duo)であるが， この計算での0.47秒は1.4GFLOPに相当する． 07年のMacBook(2GHz, Intel Core 2 Duo)ではさらに速くなって

bob% gcc -O3 bob.c -o bob
bob% ./bob
1000
 1000 [dim]     1.7543 [sec] #BOB
bob% gcc -O3 lapack.c -llapack -lblas -o lapack
bob% ./lapack
1000
 1000 [dim]     0.1893 [sec] #LAPACK

で，3.5GFLOPSが出ている．今(2016年)は，MacBookAir(2.2GHz, Intel Core i7)で... top500.orgが毎年２回High Performance Computerのランクを発表している． 今は，Top1は100PFlopsであるが， 初回の1994年6月の500位は0.4GFlopsで，今のlaptopがはるかに凌いでいる． まさにlaptopスパコンの時代なんですよ．

ライブラリーは世界中の計算機屋さんがよってたかって検証しているので，バグがほとんど無く，また，高速である． 初学者はライブラリーを使うべきである．ただし，下のサンプルプログラムの行列生成の違いのように，ブラックボックス化すると思わぬ間違い（ここではFortranとCでの行列の並び順の違いが原因)をしでかすことがあるので，プログラムに組み込む前に必ず小さい次元(サンプルコード)で検証しておくこと\footnote{少し前(2002年ごろ)GotoBLASが開発されて，性能が10%ほども上がった}．

添付のコードはちょっと長いが時間があればフォローせよ．コンパイルは，OSXでは

> gcc -O3 -UPRINT lapack.c -llapack -lblas

とすればできる．linuxではLAPACK, BLASがインストールされていれば，

> #include <vecLib/vecLib.h>

をコメントアウトして，

> gcc -O3 -DPRINT lapack.c -L/usr/local/lib64 -llapack -lblas -lg2c

などとすればコンパイルできるはず．

リスト: 西谷製lazy逆行列計算プログラム

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>

//#undef PRINT
//#define PRINT

void printMatrix(double *a, double *b, long n);
int MatrixInverse(double *a, double *b, long n);

int main(void){
  clock_t start, end;
  int i,j;
  long n;
  double *a,*b;

  scanf("%ld",&n);

  a=(double *)malloc(n*n*sizeof(double));
  b=(double *)malloc(n*sizeof(double));

  for (i=0;i<n;i++){
    for (j=0;j<n;j++){
      a[i*n+j]= 2*(double) random() / RAND_MAX - 1.0;
    }
  }
  for (i=0;i<n;i++){
    b[i]= 2*(double) random() / RAND_MAX - 1.0;
  }
  printMatrix(a,b,n);

  start = clock();
  MatrixInverse(a,b,n);
  end = clock();
  printf("%5d [dim] %10.4f [sec] #BOB\n", 
	 n,(double)(end-start)/CLOCKS_PER_SEC);
  printMatrix(a,b,n);

  free(a);
  free(b);
  return 0;
}

int MatrixInverse(double *a, double *b, long n){
  double *x;
  double pvt=0.00005,am;
  int i,j,k;

  x=(double *)malloc(n*sizeof(double));

  for(i=0;i<n-1;i++){
    if(fabs(a[i*n+i])<pvt){
      printf("Pivot %3d=%10.5f is too small.\n",i,a[i*n+i]);
      return 1;
    }
    for(j=i+1;j<n;j++){
      am=a[j*n+i]/a[i*n+i];
      for(k=0;k<n;k++) a[j*n+k]-=am*a[i*n+k];
      b[j]-=am*b[i];
    }
  }
  //Backward substitution
  for(j=n-1;j>=0;j--){
    x[j]=b[j];
    for(k=j+1;k<n;k++){
      x[j]-=a[j*n+k]*x[k];
    }
    b[j]=x[j]/=a[j*n+j];
  }
  free(x);
  return 0;
}

void printMatrix(double *a, double *b, long n){
  int i,j;
#ifdef PRINT
  printf("\n");
  for (i=0;i<n;i++){
    for (j=0;j<n;j++){
      printf("%10.5f",a[i*n+j]);
    }
    printf(":%10.5f",b[i]);
    printf("\n");
  }
  printf("\n");
#endif
  return;
}

リスト : LAPACK謹製smart逆行列計算プログラム

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>

//#define PRINT
//#undef PRINT

void printMatrix(double *a, double *b, long n);

int main(void){
  clock_t start, end;
  int i,j;
  double *a,*b;
  long n,nrhs=1, lda,ldb, info, *ipiv;

  scanf("%ld",&n);

  a=(double *)malloc(n*n*sizeof(double));
  b=(double *)malloc(n*sizeof(double));
  lda=ldb=n;
  ipiv=(long *)malloc(n*sizeof(long));
  
  for (i=0;i<n;i++){
    for (j=0;j<n;j++){
      a[j*n+i]= 2*(double) random() / RAND_MAX - 1.0;
    }
  }

  for (i=0;i<n;i++){
    b[i]= 2*(double) random() / RAND_MAX - 1.0;
  }
  printMatrix(a,b,n);

  start = clock();
  dgesv_(&n, &nrhs, a, &lda, ipiv, b, &ldb, &info);
  end = clock();
  printf("%5d [dim] %10.4f [sec] #LAPACK\n", 
	 n, (double)(end-start)/CLOCKS_PER_SEC);
  printMatrix(a,b,n);

  free(a);
  free(b);
  free(ipiv);

  return 0;
}

void printMatrix(double *a, double *b, long n){
  int i,j;
#ifdef PRINT
  printf("\n");
  for (i=0;i<n;i++){
    for (j=0;j<n;j++){
      printf("%10.5f",a[i*n+j]);
    }
    printf(":%10.5f",b[i]);
    printf("\n");
  }
  printf("\n");
#endif
  return;
}

1. 4x4の行列を適当に作り，Mapleで固有値を求めよ．求め方はマニュアルを参照せよ．
2. Jacobi法によって固有値を求めよ．
3. LAPACKに含まれているdsyev関数を用いて実対称行列の固有値を求めよ．(演習で詳しく取り上げている．研究や今後のために必要と思うときは，テキストを取りにおいで)