補間(interpolation)と数値積分(Integral)
- 概要:補間と近似
- 多項式補間(polynomial interpolation)
- Lagrange(ラグランジュ) の内挿公式
- Newton(ニュートン) の差分商公式
- 数値積分 (Numerical integration)
- 数値積分のコード
- 課題
- 解答例
補間(interpolation)と数値積分(Integral)
概要:補間と近似
単純な2次元データについて補間と近似を考える.補間はたんに点をつなぐことを,近似はある関数にできるだけ近くなるようにフィットすることを言う.補間はIllustratorなどのドロー系ツールで曲線を引くときの,ベジエやスプライン補間の基本となる.本章では補間とそれに密接に関連した積分について述べる.
| 補間と近似の模式図. |
多項式補間(polynomial interpolation)
データを単純に多項式で補間する方法を先ず示そう.$N+1$点をN次の多項式でつなぐ.この場合の補間関数は,
$$ F \left(x \right)={\sum_{i=0}^{N} } a _{i }x ^{i }=a_{0}+a_{1}x +a_{2}x^{2}+\cdots +a_{N}x^{N} $$である.データの点を$(x_{i},\,y_{i}),i=0..N$とすると
$$ \begin{array}{cl} a _{0}+a _{1}x _{0}+a _{2}x _{0}^{2}+\cdots +a _{N }x _{0}^{N }& =y _{0}\\ a _{0}+a _{1}x _{1}+a _{2}x _{1}^{2}+\cdots +a _{N }x _{1}^{N }& =y _{1}\\ \vdots& \\ a _{0}+a _{1}x _{N}+a _{2}x _{N}^{2}+\cdots +a _{N }x _{N}^{N }& =y _{N} \end{array} $$が,係数 $a_i$を未知数と見なした線形の連立方程式となっている.係数行列は
$$ A=\left[ \begin{array}{ccccc} 1&x_0&x_0^2&\cdots&x_0^N \\ 1&x_1&x_1^2&\cdots&x_1^N \\ \vdots& & & & \vdots \\ 1&x_N&x_N^2&\cdots&x_N^N \end{array} \right] $$となる.$a_i$と$y_i$をそれぞれベクトルとみなすと
により未知数ベクトル$a_i$が求まる.これは単純に,前に紹介した Gauss の消去法や LU 分解で解ける.
Mapleによる多項式補間の実例
> restart; X:=[0,1,2,3]: Y:=[1,2,3,-2]:
> with(LinearAlgebra):
> list1:=[X,Y];> with(plots):
l1p:=listplot(Transpose(Matrix(list1))):
display(l1p);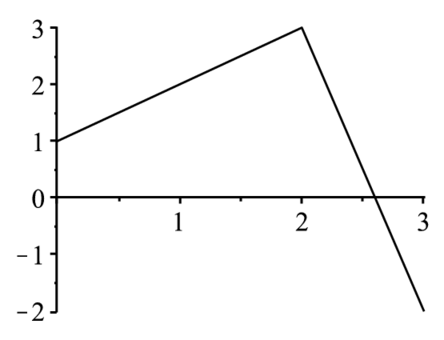 |
> A:=Matrix(4,4):
for i from 1 to 4 do
for j from 1 to 4 do
A[i,j]:=X[i]^(j-1);
end do;
end do:
A;> a1:=MatrixInverse(A).Vector(Y);> f1:=unapply(add(a1[ii]*x^(ii-1),ii=1..4),x);> f1p:=plot(f1(x),x=0..3):
l1p:=listplot(Transpose(Matrix(list1))):
display(f1p,l1p);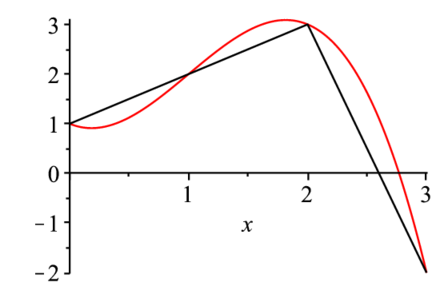 |
Lagrange(ラグランジュ) の内挿公式
多項式補間は手続きが簡単であるため,計算間違いが少なく,プログラムとして組むのに適している.しかし,あまり"みとうし"のよい方法とはいえない.その点,Lagrange(ラグランジュ)の内挿公式は見通しがよい.これは
$$ F(x)= \sum_{k=0}^N \frac{ \prod_{j \ne k} (x-x_j)} { \prod_{j \ne k} (x_k-x_j)} y_k =\sum_{k=0}^N \frac{ \frac{ (x-x_0)(x-x_1)\cdots(x-x_N)}{ (x-x_k)}} {\frac{ (x_k-x_0)(x_k-x_1)\cdots(x_k-x_N)}{ (x_k-x_k)}} y_k $$と表わされる.数学的に 2つ目の表記は間違っているが,先に割り算を実行すると読み取って欲しい.これは一見複雑に見えるが,単純な発想から出発している.求めたい関数$F(x)$を
$$ F(x) = y_0 L_0(x)+y_1 L_1(x)+y_2 L_2(x) $$とすると
$$ \begin{array}{ccc} L_0(x_0) = 1 &L_0(x_1) = 0 &L_0(x_2) = 0 \\ L_1(x_0) = 0 &L_1(x_1) = 1 &L_1(x_2) = 0 \\ L_2(x_0) = 0 &L_2(x_1) = 0 &L_2(x_2) = 1 \end{array} $$となるように関数$L_i(x)$を決めればよい.これを以下のようにとればLagrangeの内挿公式となる.
Newton(ニュートン) の差分商公式
もう一つ有名なNewton(ニュートン) の内挿公式は,
$$ \begin{array}{rc} F (x )&=F (x _{0})+ (x -x _{0})f _{1}\lfloor x_0,x_1\rfloor+ (x -x _{0})(x -x _{1}) f _{2}\lfloor x_0,x_1,x_2\rfloor + \\ & \cdots + \prod_{i=0}^{n-1} (x-x_i) \, f_n \lfloor x_0,x_1,\cdots,x_n \rfloor \end{array} $$となる.ここで$f_i \lfloor\, \rfloor$ は次のような関数を意味していて,
$$ \begin{array}{rl} f _{1}\lfloor x_0,x_1\rfloor &= \frac{y_1-y_0}{x_1-x_0} \\ f _{2}\lfloor x_0,x_1,x_2\rfloor &= \frac{f _{1}\lfloor x_1,x_2\rfloor- f _{1}\lfloor x_0,x_1\rfloor}{x_2-x_0} \\ \vdots & \\ f _{n}\lfloor x_0,x_1,\cdots,x_n\rfloor &= \frac{f_{n-1}\lfloor x_1,x_2\cdots,x_{n}\rfloor- f _{n-1}\lfloor x_0,x_1,\cdots,x_{n-1}\rfloor}{x_n-x_0} \\ \end{array} $$差分商と呼ばれる.得られた多項式は,Lagrange の内挿公式で得られたものと当然一致する.Newtonの内挿公式の利点は,新たなデータ点が増えたときに,新たな項を加えるだけで,内挿式が得られる点である.
Newton補間と多項式補間の一致の検証
関数$F(x)$を$x$の多項式として展開.その時の,係数の取るべき値と,差分商で得られる値が一致.
> restart: F:=x->f0+(x-x0)*f1p+(x-x0)*(x-x1)*f2p;> F(x1);
sf1p:=solve(F(x1)=f1,f1p);f20の取るべき値の導出
> sf2p:=solve(F(x2)=f2,f2p);
fac_f2p:=factor(subs(f1p=sf1p,sf2p));ニュートンの差分商公式を変形
> ff11:=(f0-f1)/(x0-x1);
ff12:=(f1-f2)/(x1-x2);
ff2:=(ff11-ff12)/(x0-x2);
fac_newton:=factor(ff2);二式が等しいかどうかをevalbで判定
> evalb(fac_f2p=fac_newton);数値積分 (Numerical integration)
積分,
$$ I = \int_a^b f(x) dx $$を求めよう.1次元の数値積分法では連続した領域を細かい短冊に分けて,それぞれの面積を寄せ集めることに相当する.分点の数を N とすると,
$$ \begin{array}{c} x_i = a+ \frac{b-a}{N} i = a + h \times i \\ h = \frac{b-a}{N} \end{array} $$ととれる.そうすると,もっとも単純には,
$$ I_N = \left\{\sum_{i=0}^{N-1} f(x_i)\right\}h = \left\{\sum_{i=0}^{N-1} f(a+i \times h)\right\}h $$となる.
| 数値積分の模式図. |
中点則 (midpoint rule)
中点法 (midpoint rule) は,短冊を左端から書くのではなく,真ん中から書くことに対応し,
$$ I_N = \left\{\sum_{i=0}^{N-1}f\left(a+\left(i+\frac{1}{2}\right) \times h\right)\right\}h $$となる.
台形則 (trapezoidal rule)
さらに短冊の上側を斜めにして,短冊を台形にすれば精度が上がりそうに思う. その場合は,短冊一枚の面積$S_i$は,
$$ S_i = \frac{f(x_i)+f(x_{i+1})}{2}h $$で求まる.これを端から端まで加えあわせると,
$$ i_N =\sum _{i=0}^{N-1}S_i =h \left\{ \frac{1}{2} f ( x_0 ) +\sum _{i=1}^{N-1}f ( x_i ) +\frac{1}{2} f \left( x_N \right) \right\} $$が得られる.
Simpson(シンプソン)則
Simpson(シンプソン) 則では,短冊を2次関数,
$$ f(x) = ax^2+bx+c $$で近似することに対応する.こうすると,
$$ S_i=\int _{x_i}^{x_{i+1}}f ( x )\, {dx}=\int _{x_i}^{x_{i+1}}(ax^2+bx+c)\,{dx} $$| Simpson則の導出(数式変形). |
となる.これより,
$$ I_N=\frac{h}{6} \left\{ f \left( x_0 \right) +4\,\sum _{i=0}^{N-1}f \left( x_i+\frac{h}{2} \right) +2\,\sum_{i=1}^{N-1}f \left( x_i \right) +f \left( x_N \right) \right\} $$として計算できる.ただし,関数値を計算する点の数は台形則などの倍となっている.
教科書によっては,分割数$N$を偶数にして,点を偶数番目 (even) と奇数番目 (odd) に分けて,
$$ I_{{N}}=\frac{h}{3} \left\{ f \left( x_{{0}} \right) +4\,\sum _{i={\it even}}^{N-2}f \left( x_{{i}}+\frac{h}{2} \right) +2\,\sum _{i={\it odd}}^{N-1}f \left( x_{{i}} \right) +f \left( x_{{N}} \right) \right\} $$としている記述があるが,同じ計算になるので誤解せぬよう.
数値積分のコード
次の積分を例に,Mapleのコードを示す.
$$ \int_0^1 \frac{4}{1+x^2} \, dx $$先ずは問題が与えられたらできるだけMapleで解いてしまう.答えをあらかじめ知っておくと間違いを見つけるのが容易.プロットしてみる.
> restart;
f1:=x->4/(1+x^2);
plot(f1(x),x=0..5);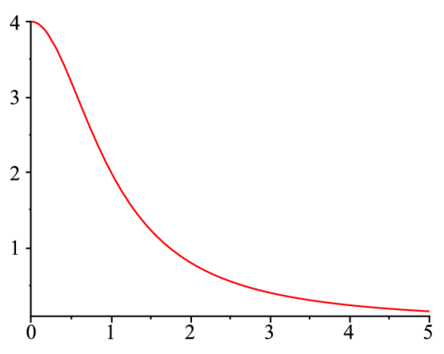 |
Mapleで解いてみる.
>int(f1(x),x=0..1);えっと思うかも知れないが,
>int(1/(1+x^2),x);となるので,納得できるでしょう.
具体的にMapleでコードを示す.先ずは初期設定.
>N:=8: x0:=0: xn:=1: Digits:=20:Midpoint rule(中点法)
> h:=(xn-x0)/N: S:=0:
for i from 0 to N-1 do
xi:=x0+(i+1/2)*h;
dS:=h*f1(xi);
S:=S+dS;
end do:
evalf(S);Trapezoidal rule(台形公式)
> h:=(xn-x0)/N: S:=f1(x0)/2:
for i from 1 to N-1 do
xi:=x0+i*h;
dS:=f1(xi);
S:=S+dS;
end do:
S:=S+f1(xn)/2:
evalf(h*S);Simpson's rule(シンプソンの公式)
> M:=N/2: h:=(xn-x0)/(2*M): Seven:=0: Sodd:=0:
for i from 1 to 2*M-1 by 2 do
xi:=x0+i*h;
Sodd:=Sodd+f1(xi);
end do:
for i from 2 to 2*M-1 by 2 do
xi:=x0+i*h;
Seven:=Seven+f1(xi);
end do:
evalf(h*(f1(x0)+4*Sodd+2*Seven+f1(xn))/3);課題
- 補間と近似の違いについて,適切な図を描いて説明せよ.
- 次の4点
x y
0 1
1 2
2 3
3 -2を通る多項式を以下のそれぞれの手法で求めよ.(a) 逆行列, (b)ラグランジュ補間, (c)ニュートンの差分商公式
$\tan(5^\circ)=0.08748866355$, $\tan(10^\circ)=.1763269807$, $\tan(15^\circ)=.2679491924$の値を用いて,ラグランジュ補間法により,$\tan(17^\circ)$の値を推定せよ.(2008年度期末試験)
(対数関数のニュートンの差分商補間:2014期末試験,25点)
2を底とする対数関数(Mapleでは$\log[2](x)$)の$F(9.2)=2.219203$をニュートンの差分商補間を用いて求める.ニュートンの内挿公式は,
$$ \begin{array}{rc} F (x )&=F (x _{0})+ (x -x _{0})f _{1}\lfloor x_0,x_1\rfloor+ (x -x _{0})(x -x _{1}) f _{2}\lfloor x_0,x_1,x_2\rfloor + \\ & \cdots + \prod_{i=0}^{n-1} (x-x_i) \, f_n \lfloor x_0,x_1,\cdots,x_n \rfloor \end{array} $$である.ここで$f_i \lfloor\, \rfloor$ は次のような関数を意味していて, f _{1}\lfloor x_0,x_1\rfloor &=& \frac{y_1-y_0}{x_1-x_0} \\ f _{2}\lfloor x_0,x_1,x_2\rfloor &=& \frac{f _{1}\lfloor x_1,x_2\rfloor- f _{1}\lfloor x_0,x_1\rfloor}{x_2-x_0} \\ \vdots & \\ f _{n}\lfloor x_0,x_1,\cdots,x_n\rfloor &=& \frac{f_{n-1}\lfloor x_1,x_2\cdots,x_{n}\rfloor- f _{n-1}\lfloor x_0,x_1,\cdots,x_{n-1}\rfloor}{x_n-x_0} \\ 差分商と呼ばれる.$x_k=8.0,9.0,10.0,11.0$をそれぞれ選ぶと,差分商補間のそれぞれの項は以下の通りとなる.
$$ \begin{array}{ccl|lll} \hline k & x_k & y_k=F_0( x_k) &f_1\lfloor x_k,x_{k+1}\rfloor & f_2\lfloor x_k,x_{k+1},x_{k+2}\rfloor & f_3\lfloor x_k,x_{k+1},x_{k+2},x_{k+3}\rfloor \\ \hline 0 & 8.0 & 2.079442 & & &\\ & & & 0.117783 & &\\ 1 & 9.0 & 2.197225 & & [ XXX ] &\\ & & & 0.105360 & & 0.0003955000 \\ 2 & 10.0 & 2.302585 & & -0.0050250 &\\ & & & 0.095310 & &\\ 3 & 11.0 & 2.397895 & & &\\ \hline \end{array} $$それぞれの項は,例えば,
$$ f_2\lfloor x_1,x_2,x_3 \rfloor =\frac{0.095310-0.105360}{11.0-9.0}=-0.0050250 $$で求められる.ニュートンの差分商の一次多項式は
$$ F(x)=F_0(8.0)+(x-x_0)f_1\lfloor x_1,x_0\rfloor =2.079442+0.117783(9.2-8.0)=2.220782 $$となる.
- 差分商補間の表中の開いている箇所[ XXX ]を埋めよ.
- ニュートンの二次多項式
の値を求めよ.
- ニュートンの三次多項式の値を求めよ.
ただし,ここでは有効数字7桁程度はとるように.(E.クライツィグ著「数値解析」(培風館,2003), p.31, 例4改)
- exp(0)=1.0, exp(0.1)=1.1052, exp(0.3)=1.3499の値を用いて,ラグランジュ補間法により,exp(0.2)の値を推定せよ.(2009年度期末試験)
- 次の関数
を$x = 0..1$で数値積分する.
- $N$を2,4,8,…256ととり,$N$個の等間隔な区間にわけて中点法で求めよ.(15)
- 小数点以下10桁まで求めた値3.141592654との差をdXとする.dXと分割数Nとを両対数プロット(loglogplot)して比較せよ(10)
(2008年度期末試験)
- 次の関数
を$x = 0..1$で等間隔に$N+1$点とり,$N$個の区間にわけて数値積分で求める.$N$を2, 4, 8, 16, 32, 64, 128, 256と取ったときの(a)中点法, (b)台形公式, (c)シンプソン公式それぞれの収束性を比較せよ.
ヒント:Maple script にあるそれぞれの数値積分法を関数 (procedure) に直して,for-loop で回せば楽.出来なければ,一つ一つ手で変えても OK. 両対数プロット (loglogplot) すると見やすい.
解答例
- 解答例[2.]
少し違うデータの場合の結果を以下に示す.データの組は以下のとおり.
> restart;
X:=[0,1,3,2];
Y:=[1,2,-2,3];
with(LinearAlgebra):
list1:=[X,Y];グラフにすると次の通り.
> with(plots):
l1p:=pointplot(Transpose(Matrix(list1))):
display(l1p);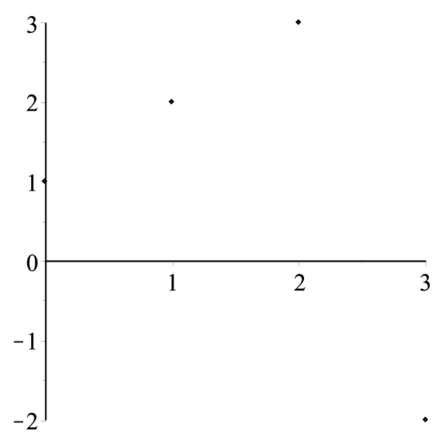 |
2次,3次までの関数をそれぞれF2,F3として,Newtonの差分商公式を使った関数を定義する.
> F2:=y0+(x-x0)*f1_01+(x-x0)*(x-x1)*f2_012;
F3:=y0+(x-x0)*f1_01+(x-x0)*(x-x1)*f2_012+(x-x0)*(x-x1)*(x-x2)*f3_0123;差分商$f_1, f_2, f_3$の公式をそのまま書き下す.
> f1_01:=(y1-y0)/(x1-x0);
f1_12:=(y2-y1)/(x2-x1);
f1_23:=(y3-y2)/(x3-x2);> f2_012:=(f1_12-f1_01)/(x2-x0);
f2_123:=(f1_23-f1_12)/(x3-x1);> f3_0123:=(f2_123-f2_012)/(x3-x0); こうすると$F_2$は
F2;となる.さて,データを追加.次の||はx0,x1,x2,x3を作る.
> for i from 1 to 4 do
x||(i-1):=X[i];
y||(i-1):=Y[i];
end:値を入れるとF2,F3は簡単な数式となる.
F2;
F3;> eq2:=expand(F2);
eq3:=expand(F3);これでNewtonの差分商公式による内挿関数が求まっている.プロットすると次の通り.
> with(plots):
l1p:=pointplot(Transpose(Matrix(list1))):
pf2:=plot(eq2,x=0..3,color=blue):
pf3:=plot(eq3,x=0..3):
display(l1p,pf2,pf3);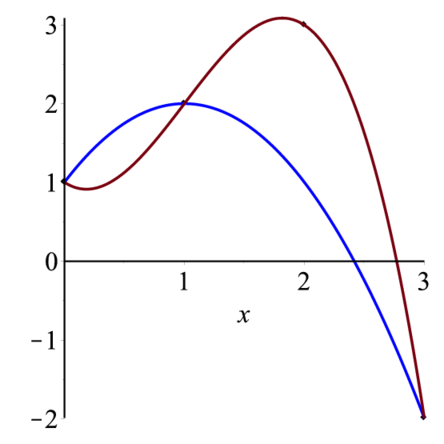 |
- 解答例[6.]
関数を定義.
> restart;
f1:=unapply(4/(1+x^2),x);plotしてみる.
> plot(f1(x),x);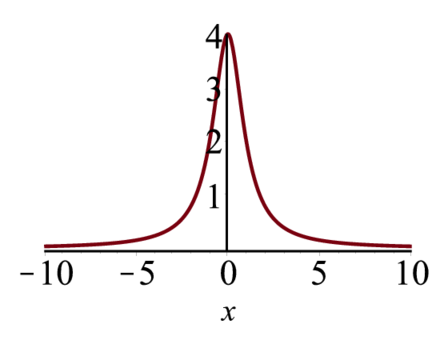 |
Mapleで答えを確認.
> int(f1(x),x=0..1);中点公式をcopyする.幾つかの初期値を設定.
> N:=8: x0:=0: xn:=1: Digits:=20:
> mid:=proc(N)
global x0,xn;
local S,i,dS,h,xi;
h:=(xn-x0)/N:
S:=0:
for i from 0 to N-1 do
xi:=x0+(i+1/2)*h;
dS:=h*f1(xi);
S:=S+dS;
end do:
evalf(S);
end;resultsという配列を用意して,分割点の数と中点公式で得られた結果をためていく.正しい答え($\pi$)との差をとるが,あとでloglogplotするので,誤差の絶対値をためておく.
> results:=[];
for i from 1 to 8 do
results:=[op(results),[2^i,evalf(abs(mid(2^i)-Pi))]];
end:loglogplotの結果.正しい解への収束の様子が表示される.
with(plots):
loglogplot([results]);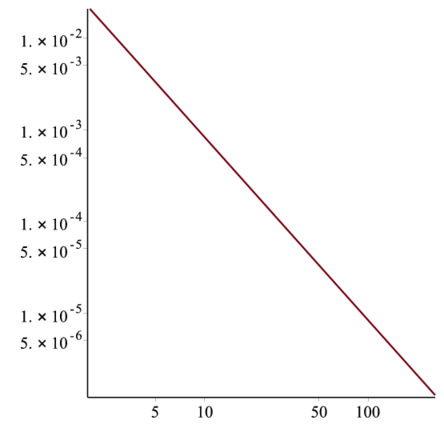 |
Keyword(s):
References:[NumMapleTOC] [SideMenu]