EqManip(式変形)

数式の変形は，手で直すほうが圧倒的に早くきれいになる場合が多い．しかし，テイラー展開や，複雑な積分公式，三角関数とexp関数の変換などの手間がかかるところを，Mapleは間違いなく変形してくれる．ここで示すコマンドを全て覚える必要は全くない．というか忘れるもの．ここでは，できるだけコンパクトにまとめて，悩んだときに参照できるようにする．初めての人は，ざっと眺めた後，鉄則からじっくりフォローせよ．

caption:数式処理で頻繁に使うコマンド．

式の変形	式の分割抽出	省略操作，その他	代入，置換，仮定
simplify:簡単化	lhs, rhs:左辺，右辺	｜｜:連結作用素	subs:一時的代入
expand:展開	numer, denom:分子，分母	seq:for-loopの簡易表記	restart,a:='a':初期化
factor:因数分解	coeff:係数	map:関数の要素への適用	assume:仮定
normal:約分・通分	nops, op	add,mul:単純な和，積	assuming:一時的仮定
combine:公式でまとめる		sum,product:数式に対応した和，積	assign:値の確定
collect:次数でまとめる		limit:極限	about:仮定の中身
sort:昇べき，降べき			anames('user'):使用変数名
rationalize:分母の有理化
convert:形式の変換

このほかにも，solve(解), diff(微分), int(積分)，series(級数展開)等は頻繁に数式の導出・変形に登場する．

簡単化(simplify)

> simplify(exp1,副関係式):
> simplify(3*x+4*x+2*y);

$$ 7\,x+2\,y $$

> exp1:=3*sin(x)^3-sin(x)*cos(x)^2; 
> simplify(exp1);

$$ {\it exp1}\, := \,3\, \left( \sin \left( x \right) \right) ^{3}-\sin \left( x \right) \left( \cos \left( x \right) \right) ^{2} \notag \\ - \left( 4\, \left( \cos \left( x \right) \right) ^{2}-3 \right) \sin \left( x \right) \notag $$

> simplify(exp1,{cos(x)^2=1-sin(x)^2});

$$ 4\, \left( \sin \left( x \right) \right) ^{3}-\sin \left( x \right) $$

オプションとしてsizeを指定するとより簡単になる場合がある．

> simplify(exp1,size):

展開(expand)

> expand((x+y)^2);

$$ {x}^{2}+2\,xy+{y}^{2} $$

因数分解(factor)

> factor(4*x^2-6*x*y+2*y^2);

$$ 2\, \left( 2\,x-y \right) \left( x-y \right) $$

約分・通分(normal)

> normal((x+y)/(x^2-3*x*y-4*y^2));

$$ \frac{1}{ x-4\,y } $$

> normal(1/x+1/y);

$$ {\frac {y+x}{xy}} $$

項を変数でまとめる(collect)

> collect(4*a*x^2-3*y^2/x+6*b*x*y+3*c*y+2*y^2,y);

$$ \left( -3\,{x}^{-1}+2 \right) {y}^{2}+ \left( 6\,bx+3\,c \right) y+4\,a{x}^{2} $$

項を公式でまとめる(combine)

> combine(sin(x)^2+3*cos(x)^2);

$$ 2+\cos \left( 2\,x \right) $$

昇べき，降べき(sort)

> sort(exp1,[x,y]); 
> sort(exp1, [x],opts);
opts=tdeg(総次数順), plex(辞書式順), ascending(昇順), descending(降順)

> exp1:=x^3+4*x-3*x^2+1: 
> sort(exp1);

$$ {x}^{3}-3\,{x}^{2}+4\,x+1 $$

> sort(exp1,[x],ascending);

$$ 1+4\,x-3\,{x}^{2}+{x}^{3} $$

> exp2:=x^3-a*x*y+4*x^2+y^2: 
> sort(exp2);

$$ -axy+{x}^{3}+4\,{x}^{2}+{y}^{2} $$

> sort(exp2,[x]);

$$ {x}^{3}+4\,{x}^{2}-ayx+{y}^{2} $$

> sort(exp2,[a,y]); 
> sort(exp2,[a],plex);

$$ -xay+{y}^{2}+{x}^{3}+4\,{x}^{2} \notag \\ -xya+{x}^{3}+4\,{x}^{2}+{y}^{2} \notag $$

分母の有理化(rationalize)

> eq1:=(1+sqrt(2))/(1-sqrt(3));

分母の有理化は，この式を $$ {\frac {1+\sqrt {2}}{1-\sqrt {3}}}{\frac {1+\sqrt {3}}{1+\sqrt {3}}} $$ とする事に対応します．

> rationalize(eq1);

$$ -1/2\, \left( 1+\sqrt {2} \right) \left( 1+\sqrt {3} \right) $$

1. 以下の式を簡単化せよ．

i) $x^{100}-1$, ii) $x^2-y^2+2x+1$, iii) $(a+b+c)^3-(a^3+b^3+c^3)$

> factor(x^100-1);

$$ \left( x-1 \right) \left( 1+{x}^{4}+{x}^{3}+{x}^{2}+x \right) \left( 1+{x}^{20}+{x}^{15}+{x}^{10}+{x}^{5} \right) \notag \\ \left( 1+x \right) \left( 1-x+{x}^{2}-{x}^{3}+{x}^{4} \right) \left( 1-{x}^{5}+{x}^{10}-{x}^{15}+{x}^{20} \right) \notag \\ \left( 1+{x}^{2} \right) \left( {x}^{8}-{x}^{6}+{x}^{4}-{x}^{2}+1 \right) \left( {x}^{40}-{x}^{30}+{x}^{20}-{x}^{10}+1 \right) \notag $$

> factor( x^2-y^2+2*x+1);

$$ \left( x+1+y \right) \left( x+1-y \right) $$

> factor((a+b+c)^3-(a^3+b^3+c^3));

$$ 3\, \left( b+c \right) \left( c+a \right) \left( a+b \right) $$

形式の変換(convert(exp1,opt))

数式の記述形式を変えるのに頻繁に使う．

opt	意味
polynom	級数を多項式(polynomial)に
trig	三角関数(trigonal)に
sincos	tanを含まない，sin,cosに
exp	指数関数形式に
parfrac	部分分数(partial fraction)に
rational	浮動小数点数を有理数形式に

> s1:=series(sin(x),x,4);
> convert(s1,polynom);

$$ {\it s1}\, := \,x-\frac{1}{6}\,{x}^{3}+O \left( {x}^{4} \right) \notag \\ x-\frac{1}{6}\,{x}^{3} \notag $$

> convert(sin(x),exp);

$$ -\frac{1}{2}\,I\left( \exp(Ix)-\exp(-Ix) \right) $$

> convert(sinh(x),exp);

$$ \frac{1}{2}\,\exp(x)-\frac{1}{2}\,\exp(x) $$

> convert(tan(x),sincos);

$$ {\frac {\sin \left( x \right) }{\cos \left( x \right) }} $$

> convert(exp(I*x),trig);

$$ \cos \left( x \right) +I\sin \left( x \right) $$

> convert(1/(x-1)/(x+3),parfrac);

$$ - \frac{1}{4\left( x+3 \right) }+ \frac{1}{4 \left( x-1 \right) } $$

> convert(3.14,rational);

$$ {\frac {157}{50}} $$

左辺，右辺(lhs, rhs)

それぞれ，左辺，右辺を意味するleft hand side, right hand sideの略

> lhs(sin(x)^2=1-1/x);
> rhs(sin(x)^2=1-1/x);

$$ \sin \left( x \right)^{2} \notag \\ 1-\frac{1}{x} \notag $$

分母，分子(denom,numer)

それぞれ，分母，分子を意味するdenominator, numeratorの略

> numer(a*x/(x+y)^3);
> denom(a*x/(x+y)^3);

$$ ax \notag \\ \left( x+y \right) ^{3} \notag $$

係数(coeff)

> coeff(4*a*x^2-3*y^2/x+6*b*x*y+3*c*y+2*y^2,y^2);

$$ -\frac{3}{x}+2 $$

要素の取りだし，要素数(op, nops)

op, nopsはlist配列から要素や要素数を取り出すのに頻繁に使われる．数式を含めた，より一般的な構造に対しても作用させることができる．

> op(4*a*x^2-3*y^2/x+6*b*x*y+3*c*y+2*y^2);

$$ 4\,a{x}^{2},\,-{\frac {{3\,y}^{2}}{x}},\,6\,bxy,\,3\,cy,\,2\,{y}^{2} $$

> nops(4*a*x^2-3*y^2/x+6*b*x*y+3*c*y+2*y^2); #res: 5

1. 以下の関数をx0まわりで3次までテイラー展開し，得られた関数ともとの関数をプロットせよ．さらに高次まで展開した場合はどう変化するか．

i) $y =\cos \left(x \right),{\it x0} =0$, ii) $y =\ln\left(x \right),{\it x0} =1$, iii) $y =\exp \left(-x \right),{\it x0} =0$

1. $ \frac{x+1}{(x-1)(x^2+1)^2}$を部分分数に展開せよ．
2. $ \frac{1}{1-x^4} = \frac{a}{x^2+1}+\frac{b}{x+1}+\frac{c}{x-1}$が常に成立する$a, b, c$を定めよ．
3. $ \frac{8}{3-\sqrt{5}}-\frac{2}{2+\sqrt{5}}$を簡単化せよ．
4. $ x^2+2kx+5-k=0$が重根をもつように$k$を定めよ．

1. seriesでTaylor展開した後，convertで多項式(polynom)に変換する．

> convert(series(cos(x),x),polynom);

$$ 1-\frac{1}{2}\,{x}^{2}+\frac{1}{24}\,{x}^{4} $$

> plot([convert(series(cos(x),x),polynom),cos(x)],x=-Pi..Pi);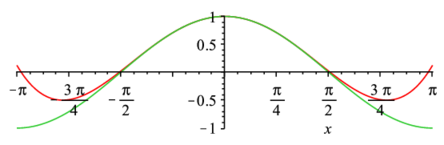

$$ 1-\frac{1}{2}\,{x}^{2}+\frac{1}{24}\,{x}^{4}-{\frac {1}{720}}\,{x}^{6}+{\frac {1}{40320}}\,{x}^{8} $$

高次展開する場合には，seriesの最後の引数に次数を指定する．デフォルトは6次．関数の一致具合が向上していることに注目．

convert(series(cos(x),x,9),polynom);
plot([convert(series(cos(x),x,9),polynom),cos(x)],x=-Pi..Pi);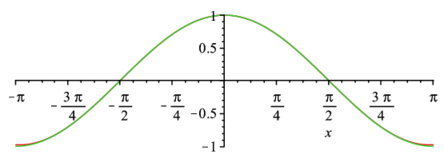

seriesでの展開で，x=1とするとその周りでの展開になる．

> convert(series(ln(x),x=1),polynom);

$$ x-1-\frac{1}{2}\, \left( x-1 \right) ^{2}+\frac{1}{3}\, \left( x-1 \right) ^{3}-\frac{1}{4}\, \left( x-1 \right) ^{4}+\frac{1}{5}\, \left( x-1 \right) ^{5} $$

> plot([convert(series(ln(x),x=1),polynom),ln(x)],x=0..2);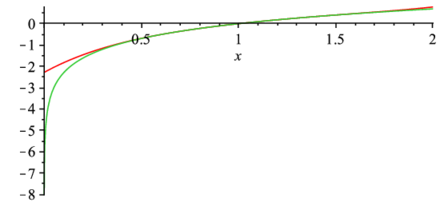

> convert(series(exp(-x),x),polynom);

$$ 1-x+\frac{1}{2}\,{x}^{2}-\frac{1}{6}\,{x}^{3}+\frac{1}{24}\,{x}^{4}-{\frac {1}{120}}\,{x}^{5} $$

> plot([convert(series(exp(-x),x),polynom),exp(-x)],x=0..2);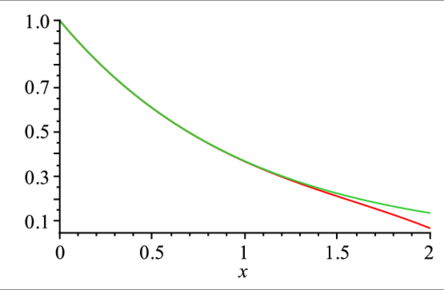

> restart; eq1:=(x+1)/((x-1)*(x^2+1)^2);

$$ {\it eq1}\, := \,{\frac {x+1}{ \left( x-1 \right) \left( {x}^{2}+1 \right) ^{2}}} $$

> convert(eq1,parfrac);

$$ \frac{1}{2 \left(x-1 \right) }-{\frac {x}{ \left( {x}^{2}+1 \right) ^{2}}}+\frac{1}{2}\,{\frac {-x-1}{{x}^{2}+1}} $$

> convert(1/(1-x^4),parfrac);

$$ - \frac{1}{4 \left( x-1 \right)}+ \frac{1}{ 4\,\left(x+1 \right) }+ \frac{1}{2\,\left( {x}^{2}+1 \right)} $$

> eq2:=8/(3-sqrt(5))-2/(2+sqrt(5));

$$ {\it eq2}\, := \frac{8}{3- \sqrt{5}}-\frac{2}{2+ \sqrt{5}} $$

まずはデフォルトの簡単化(simplify)．

> simplify(eq2); #res: 10

方程式をたてる．

> eq3:=x^2+2*k*x+(5-k);

$$ {\it eq3}\, := \,{x}^{2}+2\,kx+5-k $$

単純に解を求めて，

> sol1:=solve(eq3=0,x);

$$ {\it sol1}\, := \,-k+ \sqrt{{k}^{2}-5+k},\,-k- \sqrt{{k}^{2}-5+k} $$ それが一致する場合のkを解く． <<<maple > solve(sol1[1]=sol1[2],k); >>> $$ -\frac{1}{2}+\frac{1}{2}\, \sqrt{21},\,-\frac{1}{2}-\frac{1}{2}\, \sqrt{21} $$ 別解．まず，係数をcoeffで取り出す． <<<maple > aa:=coeff(eq3,x^2); #res:1 > bb:=coeff(eq3,x); #res: 2 k > cc:=coeff(eq3,x,0); #res: 5 - k >>> 判別式$D=b^2-4ac$を計算して，$=0$とおいてkについて解く． <<<maple > solve(bb^2-4*aa*cc=0,k); >>> $$ -\frac{1}{2}+\frac{1}{2}\, \sqrt{21},\,-\frac{1}{2}-\frac{1}{2}\, \sqrt{21} $$ !代入，置換，仮定に関連したコマンド(assume, subs) !!一時的代入(subs) 関係式(x=2)を式(exp1)に一時的に代入した結果を表示． <<<maple > exp1:=x^2-4*x*y+4; subs(x=2,exp1); >>> $$ {\it exp1}\, := \,{x}^{2}-4\,xy+4 \notag \\ 8-8\,y \notag $$ <<<maple > subs({x=a+2,y=sin(x)},exp1); >>> $$ \left( a+2 \right) ^{2}-4\, \left( a+2 \right) \sin \left( x \right) +4 $$ !!仮定(assume) 変数になにかの条件を仮定するときに使う．たとえば，根を開くときに，与式が正と仮定すると開かれる． <<<maple > sqrt(b^2); > assume(a>0); sqrt(a^2); >>> $$ \sqrt{{b}^{2}} \notag \\ a\sim \notag $$

一時的仮定(assuming)

assumeと同じだが，一時的に仮定するときに使われる．

> exp1:=x^2-4*x+4; 
> sqrt(exp1);

$$ {\it exp1}\, := \,{x}^{2}-4\,x+4 \notag \\ \sqrt{ \left( -2+x \right) ^{2}} \notag $$

> sqrt(exp1) assuming x>2;

$$ -2+x $$

assumeに加えての仮定にadditionallyがある．

solveで求めた値の確定(assign)

解を求めるsolveをして

> x:='x':y:='y': 
> s1:=solve({x-y+1=0,x+y-2=0},{x,y}); 

$$ {\it s1}\, := \, \left\{ x=\frac{1}{2},y=\frac{3}{2} \right\} $$

このまま，x,yの中身を見ても，

> x,y;

$$ x,\,y $$

代入されていない．s1をassign(確定)すると，

> assign(s1);
> x,y;

$$ \frac{1}{2},\frac{3}{2} $$

と代入される．一時的代入subsと使い分ける．

assumeで仮定した内容の確認(about)

> about(a);

Originally a, renamed a~:
  is assumed to be: RealRange(Open(0),infinity)

ユーザが定義した変数の確認(anames('user'))

> anames('user');

$$ {\it s1},\,y,\,x,\,a $$

値の初期化(restart,a:='a')

連結作用素($||$)

前後の変数をくっつけて新たな変数とする．

> a||1; #res: a1
> a||b; #res: ab

プログラムの中で使うとより便利．

> for i from 1 to 3 do
    a||i:=i^2; 
  end do;

$$ a1:=1 \notag \\ a2:=4 \notag \\ a3:=9 \notag $$

for-loopの簡略表記(seq)

数列を意味するsequenceの略．

> seq(k,k=4..7);

$$ 4,\,5,\,6,\,7 $$

リスト要素への関数の一括適用(map)

> f:=x->exp(-x); 
> map(f,[0,1,2,3]);

$$ f\, := \,x\mapsto \exp(-x) \notag \\ [1,\exp(-1),\exp(-2),\exp(-3)] \notag $$

上記の３つを組み合わせると，効率的に式を扱うことができる．

> map(sin,[seq(theta||i,i=0..3)]);

$$ [\sin \left( {\it \theta0} \right) ,\sin \left( {\it \theta1} \right) ,\sin \left( {\it \theta2}\\ \mbox{} \right) ,\sin \left( {\it \theta3} \right) ] $$

単純な和，積(add,mul)

> add(x^i,i=0..3);

$$ 1+x+{x}^{2}+{x}^{3} $$

> mul(x^i,i=0..3);

$$ {x}^{6} $$

数式にも対応した和，積(sum,product)

> add(x^i,i=0..n);

Error, unable to execute add

> sum(x^i,i=0..n);

$$ {\frac {{x}^{n+1}}{x-1}}- \frac{1}{x-1} $$

> product(x^i,i=0..n);

$$ {x}^{\frac{1}{2}\, \left( n+1 \right) ^{2}-\frac{1}{2}\,n-\frac{1}{2}} $$

極限(limit)

> limit(exp(-x),x=infinity); #res: 0

> limit(tan(x),x=Pi/2);

$$ {\it undefined} $$

> limit(tan(x),x=Pi/2,left); 
> limit(tan(x),x=Pi/2,complex);

$$ \infty \notag \\ -\infty +\infty \, I\notag $$

どうしても解かなければならない課題を前にコマンドリファレンスのあちこちを参照しながら解いていくのが数式処理を修得する最速法である．とびかかる前にちょっとした共通 のコツがある．それをここでは示す．数式処理ソフトでの数式処理とは，数式処理ソフトが『自動的にやって』くれるのではなく，実際に紙と鉛筆で解いていく手順を数式処理ソ フトに『やらせる』ことであることを肝に銘じよ．

鉄則

Mapleをはじめとする数式処理ソフトの習得にあたって初心者がつまづく共通の過ちを回避する鉄則がある．

鉄則０：restart をかける

続けて入力すると前の入力が生きている．違う問題へ移るときや，もう一度入力をし直すときには，restart;を入力して初期状態からはじめる．入力した順番が狂っている場合もある．頭から順にreturnをやり直す．

鉄則１：出力してみる

多くのテキストではページ数の関係で出力を抑止しているが，初心者が問題を解いていく段階ではデータやグラフをできるだけ多く出力する．最後のコロンをセミコロンに変える，あるいは途中にprint文を入れる．

鉄則２：関数に値を代入してみる

数値が返ってくるべき時に変数があればどこかで入力をミスっている．plotで以下のようなエラーが出た場合にチェック．

> plot(f(x),x);

Warning, unable to evaluate the function to numeric values in the region; see
the plotting command's help page to ensure the calling sequence is correct

鉄則３：内側から順に入力する

長い入力やfor-loopを頭から打ち込んではいけない！！　内側から順に何をしているか解読・確認しながら打ち込む．括弧が合わなかったり，読み飛ばしていたりというエラーが回避できる．

具体例：無限積分

以下に示す積分を実行せよ．

$$ \int _{-\infty }^{\infty }x \exp(-\beta c\,{x}^{2}) \left( 1+\beta g\,{x}^{3} \right) {dx} $$

最新版のMapleでは改良が施されていて，このような複雑な積分も一発で求まる．

> f1:=unapply(x*exp(-beta*c*x^2)*(1+beta*g*x^3),x);

$$ {\it f1}\, := \,x\mapsto x\exp(-\beta c\,{x}^{2}) \left( 1+\beta\,g{x}^{3} \right) $$

> int(f1(x),x=-infinity..infinity);

$$ \left\{\, \begin {array}{cc} { \frac{3}{4}\,\frac {g \sqrt{\pi }}{\beta\,{c}^{2} \sqrt{c\beta}}}&csgn \left( c\beta \right) =1\\ \infty&otherwise\end {array} \right. $$

ここでは，$c \beta$が正の場合(csgn(beta c)=1)とそれ以外の場合(otherwise)に分けて答えを返している．しかしこのような意図したきれいな結果をいつもMapleが返してくれるとは限らない．これだけしか知らないと，なにかうまくいかないときにお手上げになってしまう．このようなきれいで簡単な結果に行き着く前の，裏でおこなういくつかの予備計算を省略せずに示そう．

先ず鉄則０にしたがってrestartをかけ，関数を定義する．

> restart; f1:=unapply(x*exp(-beta*c*x^2)*(1+beta*g*x^3),x);

$$ $$

次には鉄則１にしたがって積分する前にどのような関数かプロットしてみる．そのままplotへ投げると怒られる．

> plot(f1(x),x=-10..10);

Warning, unable to evaluate the function to numeric values in the region; see
the plotting command's help page to ensure the calling sequence is correct

これは鉄則２にあるとおり，数値を代入すれば，

> f1(10);

$$ 10\,\exp(-100\,c\beta) \left( 1+1000\,\beta\,g \right) $$

beta,c,gなどのパラメータの値が入っていないためとわかる．適当に値を代入する．

> c:=1; g:=0.01; beta:=0.1; #res:1 0.01 0.1

再度プロットを試みる．

> plot(f1(x),x=-10..10);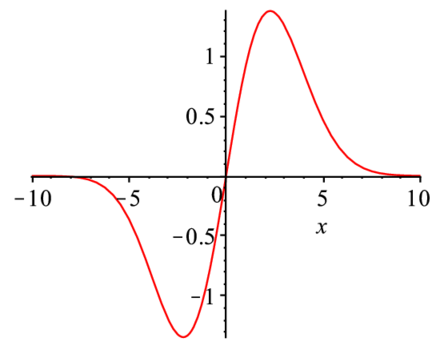

実際に積分してみる．ここでは，鉄則３にしたがって，式を頭から打ち込むのではなく内側からみていくことが肝要である．これは問題を解いていく時に，思考が必ずたどるであ ろう順番に相当する． 先ず変数に入れた数値をクリアする．

> c:='c': g:='g':beta:='beta':

不定積分でこの関数が積分できることを確認する．

> int(f1(x),x);

$$ -\frac{1}{2}\,{\frac {1}{{\exp(c\beta\,{x}^{2})}\beta\,c}}+\beta\,g \left( -\frac{1}{2}\,{\frac {{x}^{3}{ \exp(-c\beta\,{x}^{2}) }}{c\beta}}+\frac{3}{2}\, \left( -\frac{1}{2}\,{\frac {x{\exp(-c\beta\,{x}^{2})}}{c\beta}}+\frac{1}{4}\,{\frac { \sqrt{\pi }{erf\left( \sqrt{c\beta}x\right)}}{c\beta\, \sqrt{c\beta}}} \right) {c}^{-1}{\beta}^{-1} \right) $$

次にx=-alpha..alphaの定積分を実行する．これは上記のコマンドに付け足すようにしていく．

> int(f1(x),x=-alpha..alpha);

$$ -\frac{1}{4}\,{\frac {g \left( 4\,{\alpha}^{3}\exp({-c\beta\,{\alpha}^{2}}) \beta\,c \sqrt{c\beta}+6\,\alpha\,\exp({-c\beta\,{\alpha}^{2}}) \sqrt{c\beta}-3\, \sqrt{\pi }{erf\left( \sqrt{c\beta}\alpha\right)}\\ \mbox{} \right) }{\beta\,{c}^{2} \sqrt{c\beta}}} $$

さらに$\alpha \mapsto \infty$としてみる．

> limit(int(f1(x),x=-alpha..alpha),alpha=infinity);

$$ \lim _{\alpha\rightarrow \infty }-\frac{1}{4}\,{\frac {g \left( 4\,{\alpha}^{3}\exp({-c\beta\,{\alpha}^{2}})\beta\,c \sqrt{c\beta}+6\,\alpha\,\exp({-c\beta\,{\alpha}^{2}}) \sqrt{c\beta}-3\, \sqrt{\pi }{erf\left( \sqrt{c\beta}\alpha\right)} \right) \\ \mbox{}}{\beta\,{c}^{2} \sqrt{c\beta}}} $$

ところがこれでは答えを返してくれない．積分した後のそれぞれの項を見ると$\beta \,c>0$を仮定すれば簡単になることが分る．assumeを使って，このような変数の仮定おこ なう．

> assume(beta*c>0);

結果として最初に出した解答を得る．

> limit(int(f1(x),x=-alpha..alpha),alpha=infinity);

$$ \frac{3}{4}\,{\frac { \sqrt{\pi }g}{\beta \,{c}^{2} \sqrt{\beta \,c}}} $$

式のフォローのデフォルト

Mapleで実際に数式をいじる状況というのは，ほとんどの場合が既知の数式変形のフォローだろう．例えば，論文で「(1)式から(2)式への変形は自明である」とかいう 文章で済ましている変形が本当にあっているのかを確かめたい時．一番単純なやり方は自明と言われた前後の式が一致していることを確かめるだけで十分である． 最も単純な確認法は以下の通り，変形の前後の式を手入力してその差をexpandした結果が0か否かでする．

> ex1:=(x-3)^4;

$$ {\it ex1}\, := \, \left( x-3 \right) ^{4} $$

> ex2:=x^4-12*x^3+54*x^2-108*x+81;

$$ {\it ex2}\, := \,{x}^{4}-12\,{x}^{3}+54\,{x}^{2}-108\,x+81 $$

> expand(ex1-ex2); #res: 0

0ならば式の変形は保証されているので，その導出が間違いでなく誤植などもないことが確認できる．ただ，これだけでは変形の哲学や技法が身に付くわけではない．あくまでも 苦し紛れのデフォルトであることは心に留めておくように． 論理値として確かめたいときには，evalbを使う．

> evalb(expand(ex1-ex2)=0); #res: true

数式変形実践課題（大学入試センター試験の解法を通して）

今まで出てきたコマンドを使えば，典型的なセンター試験の問題を解くのも容易である．以下の例題を参照して課題を解いてみよ．使うコマンドは，unapply, solve, diff, expand(展開), factor(因数分解)とsubs(一時的代入)である．expand等の数式変形によく使うコマンドは次節以降で詳しく解説している．subsは以下を参考にせよ．

一時的代入(subs)

代入(:=)が永続的なのに対して，一時的な代入はsubsで行う．

> subs(a=1,a+2); #res: 3

典型的な使い方は，solveで求めた解などを式(equation)として代入しておいて，それをsubsで一時的に当てはめる．

> eq1:=a=solve(a+b=0,a); subs(eq1,a+2);

$$ a = -b \notag \\ -b + 2 \notag $$

例題:2次関数の頂点

$a,b$を定数とし, $a <> 0$とする．2次関数

$$ y = a\,x^2-b\,x-a+b\,\cdots(1) $$

のグラフが点 $(-2, 6)$ を通るとする.このとき

$$ b = -a+[ XXX ] $$

であり,グラフの頂点の座標を$a$を用いて表すと

$$ \left(\frac{-a+[ XXX ]}{[ XXX ]\,a}, -\frac{([ XXX ]\,a- [ XXX ])^2}{[ XXX ]\,a}\right) $$

である (2008 年度大学入試センター試験数学 I より抜粋).

解答例

まず，与えられた2次関数を$f(x)$で定義する．

> restart; f:=unapply(a*x^2-b*x-a+b,x);

$$ f\, := \,x\mapsto a\,{x}^{2}-b\,x-a+b $$

与えられた点の座標を関数に入れる．

> eq1:=f(-2)=6;

$$ {\it eq1}\, := \,3\,a+3\,b=6 $$

これをbについて解く．

> eq2:=b=solve(eq1,b);

$$ {\it eq2}\, := \,b=2-a $$

次は，頂点の座標で傾きが0になることを用いて解いていく．

> solve(diff(f(x),x)=0,x);

$$ \frac{1}{2}\,{\frac {b}{a}} $$

bの値はeq2で求まっているので，それを代入(subs)する．

> subs(eq2,solve(diff(f(x),x)=0,x));

$$ \frac{1}{2}\,{\frac {2-a}{a}} $$

これをx0としてeq3で定義しておく．

> eq3:=x0=subs(eq2,solve(diff(f(x),x)=0,x));

$$ {\it eq3}\, := \,{\it x0}=\frac{1}{2}\,{\frac {2-a}{a}} $$

頂点のy座標は，$f(x0)$で求まる

> f(x0);

$$ a\,{{\it x0}}^{2}-b\,{\it x0}-a+b $$

eq2, eq3で求まっているx0, bを代入する．

> eq4:=subs({eq2,eq3},f(x0));

$$ {\it eq4}\, := \,-\frac{1}{4}\,{\frac { \left( 2-a \right) ^{2}}{a}}-2\,a+2 $$

これを因数分解(factor)する．

> factor(subs({eq2,eq3},f(x0)));

$$ -\frac{1}{4}\,{\frac { \left( 3\,a-2 \right) ^{2}}{a}} $$

$P = x(x+3)(2x-3)$とする． また，$a$を定数とする． $x = a+1$のときの $P$の値は

$$ 2a^3+[ XXX ]a^2+[ XXX ]a-[ XXX ] $$

である．

$x=a+1$のときの$P$の値と，$x=a$のときの$P$の値が等しいとする．このとき，$a$は

$$ 3a^2+[ XXX ]a-[ XXX ] = 0 $$

を満たす．したがって

$$ a = \frac{[ XXX ]\pm \sqrt{[ XXX ]}}{[ XXX ]} $$

である.

（例題１．に引き続いて，） さらに，2次関数(1)のグラフの頂点のy座標が-2であるとする．このとき，aは

$$ [ XXX ]\,a^2-[ XXX ]\,a+[ XXX ] = 0 $$

を満たす．これより，aの値は

$$ a = [ XXX ], \frac{[ XXX ]}{[ XXX ]} $$

である． 以下，$a = \frac{[ XXX ]}{[ XXX ]}$であるとする．

このとき，2次関数(1)のグラフの頂点のx座標は[ XXX ]であり，(1)のグラフとx軸の2交点のx座標は[ XXX ],[ XXX ]である．

また，関数(1)は$0 \leqq x \leqq 9$において

$x$ = [ XXX ]のとき，最小値[ XXX ]をとり，

$x$ = [ XXX ]のとき，最大値$\frac{[ XXX ]}{[ XXX ]}$をとる．

(2008 年度大学入試センター試験数学 I より抜粋).

$P$を$x$の関数として定義，

> restart:
> P:=unapply(x*(x+3)*(2*x-3),x);

$$ P\, := \,x\mapsto x \left( x+3 \right) \left( 2\,x-3 \right) $$

$P(a+1)$および$P(a)$を形式的に出してみる．

> expand(P(a+1)), expand(P(a));

$$ 2\,{a}^{3}+9\,{a}^{2}+3\,a-4,\,2\,{a}^{3}+3\,{a}^{2}-9\,a $$

2式を差し引く．

> eq1:=(expand(P(a+1))-expand(P(a)))/2;

$$ {\it eq1}\, := \,3\,{a}^{2}+6\,a-2 $$

出題にそろえるため2で割っている．その式をeq1として代入し，eq1=0をxについて解く(solve).

> sol1:=solve(eq1=0,a);

$$ {\it sol1}\, := \,-1+\frac{1}{3}\, \sqrt{15},\,-1-\frac{1}{3}\, \sqrt{15} $$

例題のeq3,eq4までを確認 %(あるいは，ここまではEqManip_ExampleCenterExamIを打ち込む．)

> eq3, eq4;

$$ {\it x0}=\frac{1}{2}\,{\frac {2-a}{a}},\, -\frac{1}{4}\,{\frac { \left( 2-a \right) ^{2}}{a}}-2\,a+2 $$

eq4が頂点の$y$座標の値なので，これから$-2$を引いて展開．

expand((eq4-(-2)));

$$ -\frac{1}{a}+5-\frac{9}{4}\,a $$

これではわかりにくいので，出題にそう形にするため，$-4a$を掛け，eq5とする．

> eq5:=expand((eq4+2)*(-4)*a);

$$ {\it eq5}\, := \,4-20\,a+9\,{a}^{2} $$

これを$a$について解いて(solve)

> solve(eq5=0,a);

$$ 2,\,\frac{2}{9} $$

$a=2/9$をeq3に代入して，頂点の$x$座標を出す．

> subs(a=2/9,eq3);

$$ {\it x0}=4 $$

$a,b$を$f(x)$に代入して，

> eq6:=subs({a=2/9,b=2-2/9},f(x));

$$ {\it eq6}\, := \,\frac{2}{9}\,{x}^{2}-{\frac {16}{9}}\,x+{\frac {14}{9}} $$

これを解いて，$x$座標の交点を求める．

> solve(eq6=0,x);

$$ 7,\,1 $$

最大値，最小値を求めるために，今まで求めたパラメータを代入して，plotしてみる．

> plot(subs({a=2/9,b=2-2/9},f(x)),x=0..9);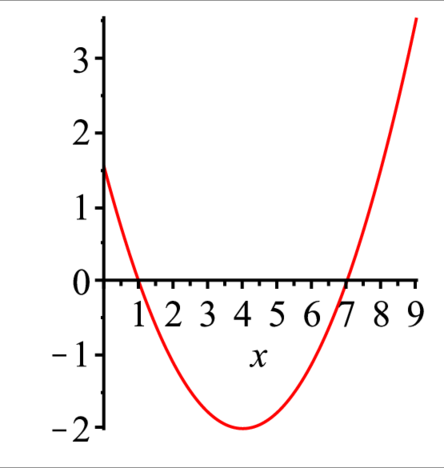

目視で分かるとおり，最小値$x=4$,最大値$x=9$で

> subs({a=2/9,b=2-2/9},f(4)), subs({a=2/9,b=2-2/9},f(9));

$$ -2,\,\frac{32}{9} $$