(..Above)離散数学，最適化理論と，それらの現実世界への応用
グラフ理論，複雑ネットワーク理論に関する研究
- 複雑ネットワークの構造に関する研究
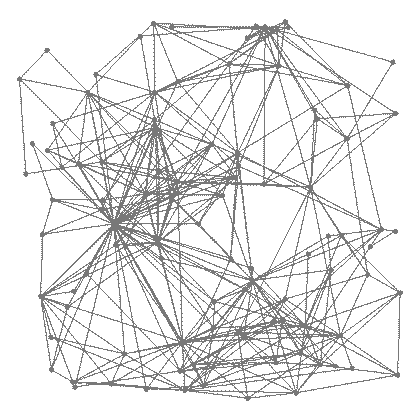WWWにおけるハイパーリンクで繋がれたドキュメント全体の構造や，インターネットの接続構造，交友関係の構造など，多くの領域にネットワーク構造が見られる．これらのネットワークの中には，まったく異なる分野で独立に形成されるものであるにも関わらず，驚くべきことに共通する性質を持つことがある．例えば，友達の友達の...とたどっていくと，全世界のほとんどの人にせいぜい数ステップで到達できるスモールワールドと呼ばれる性質や，次数分布がべき則に従うというスケールフリーと呼ばれる性質などが知られている．しかし，まったくランダムに作ったグラフは，現実のネットワークとはかなり違うものになる．では，現実のネットワークはどのような原理でできあがるのであろうか？ 少なくともまったくランダムではなく，何らかの規則性がある．それを見つけるべく，様々な数理モデルを構築し，性質を解析している．さらに，グラフ理論や確率論など，様々な理論を駆使して，本質的な性質の解明も行っている．
右図は，我々が提案した「空間閾値モデル」によって生成され描かれたネットワークの例である．簡単な規則で生成されるが，現実のネットワーク「らしい」形状になっていることが見て取れる．- 複雑ネットワークの機能に関する研究
インターネット上でコンピュータウィルスや，交友関係ネットワーク上でインフルエンザなど本物のウィルスが拡散・消滅する現象，また特に災害時のデマやうわさが広がる現象を解析して特性を明らかにすることに加え，これらを積極的にコントロールするという工学的な観点からの様々なアルゴリズムの設計を行っている．これらは，ウィルス対策方法の構築のためにも必要不可欠である．
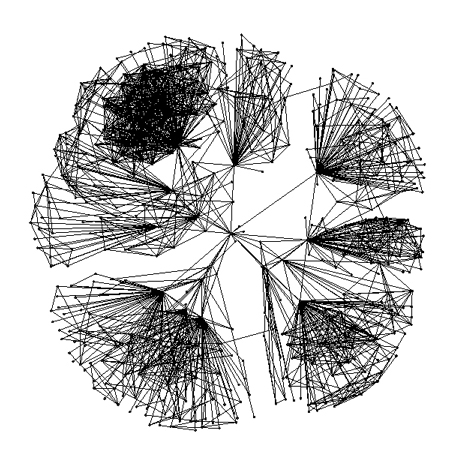
ウィルスやデマなどが消滅せずに生き残り続けるか否かは，感染力と駆除力のせめぎあい，そしてグラフ（ネットワーク）の形状で決まる．例えば，友人が多い人がコンピュータウィルスに感染すると影響力が強いため，このような人々が多いとなかなか駆除しきれないというのは想像できるであろう．ウィルスやデマを早期に発見し，その拡散を封じ込める方法を研究開発する際には，グラフ理論的・確率論的なアプローチはたいへん有効である．
右図は，本研究室で研究開発された「うわさ伝播解析システム」によるシミュレーションの描画例である．- 複雑ネットワークの検索への応用
- 検索技術とネットワークとは密接な関わりがある．最も有名な例として，Googleのページランクがある．これはWWWのハイパーリンクネットワークのグラフ構造を利用したものである．他にもコミュニティ構造を探索するなど，様々な研究がある．本研究室では，WWWのネットワークのグラフ構造の特徴を利用した検索技術を研究している．
- 複雑ネットワークのマーケティングへの応用
- 口コミネットワークを利用することで，新商品の広告コストを抑えることはできるだろうか？ できるだけ多くの消費者に高い頻度で目にしてもらうためには，どのように広告を投入すればよいだろうか？ これらの問題にも取り組んでいる．
- 複雑ネットワークの実データ収集に関する研究開発
インターネットの構造や人間関係の構造など，様々なネットワークのデータを収集することは，実際にはかなり困難である．本研究室では，ネットワークのデータそのものを効率的に収集する方法と実装に関する研究開発に加えて，限られた観測データから実ネットワークの特性を推定する方法の研究も行っている．
最適化とアルゴリズムに関する研究
- 金融工学に関する研究
- 経済システムの解析や資産運用を工学的な観点から研究している．例えば，資産を複数の株式に分散投資することによってリスクを軽減しつつも収益最大化を目指すポートフォリオ最適化や，オプションなど金融デリバティブの価格形成の解析などには，最適化理論や確率論が現れてくる．金融工学の分野には多様な問題が数多くあり，解析が待たれているが，本研究室では，これらの課題にも取り組んでいる．
- 現実の問題への最適化理論の適用
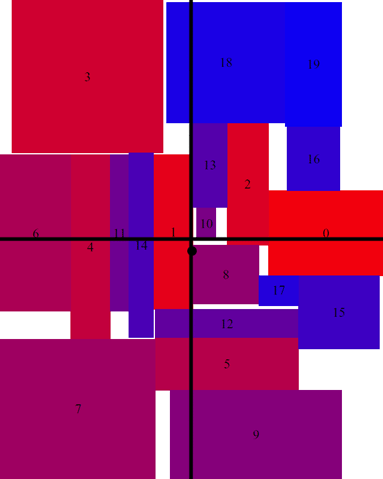世の中には数多くの最適化問題が存在する．実際，ある制約の下で何かを最適化するという枠組みで捉えられるものはいくらでも見つかる．本研究室では，そのような現実の問題に取り組み，数理的に解析すると同時に，現実的なソリューションを与えてコンサルティングすることまで行っている．例えば，車の設計問題において，複数の寸法と重量の情報を持ったモジュールに対して，制約条件の下に目的関数の値を最大(最小)にするように配置場所を決定することが必要となる．また，段ボール製造において，多くの注文を適切に並べ替えて処理することによって処理時間を短縮することが求められる．他にも，料理献立計画や，クラス編成問題など，様々な問題を扱っている．- 現実の問題への待ち行列理論の適用
- 待ち行列とは，例えばスーパーのレジの前に客が作る行列のことである．このような待ち行列で，待ち時間はどれくらいか，混雑を解消するためにはレジを増やすべきか，レジの処理速度をあげるべきかなどを考えるためには，確率論を用いた解析が必要になる．応用範囲は多岐にわたり，実用的にも重要である．例えば，通信ネットワークの容量設計や性能評価には必要不可欠である．本研究室では，通信ネットワークにおける研究以外にも，テーマパークの待ち行列制御や，渋滞を軽減する交通信号機制御に関する研究開発も行っている．
- 離散最適化に関する様々な問題
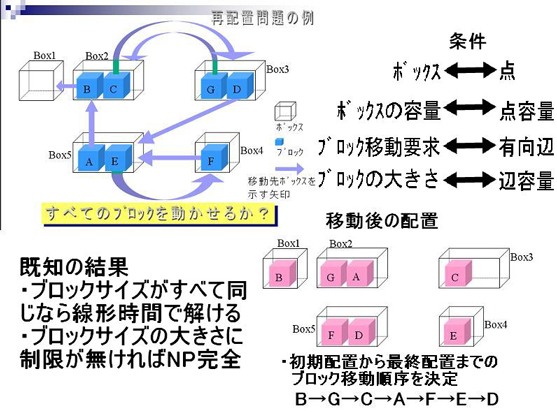例えば，巳波らが定義した再配置問題という一見パズルのようであるがメモリ配置最適化など様々な応用と関わっている離散最適化問題がある．このような様々な問題も研究している．