Powered by SmartDoc

種々のソート法の振る舞い

数式処理演習　西谷　滋人

insertソート

データを指定順に並べるソートをMapleを使ってやってみましょう．まずは簡単な挿入(insert)ソートです．実際のスクリプトは

restart;with(plots):

insertsort:=proc(A::Array) 
local n,x,i,j; 
n:=op(ArrayDims(A))[2]; 
for i from 2 to n do 
	print("B",i,A[i],A); 
	x:=A[i]; 
	for j from i-1 to 1 by -1 do 
		if (A[j] < x) then break; end if; 
		A[j+1]:=A[j]; 
	od; 
	A[j+1]:=x; 
	print("A",i,j+1,A); 
od; 
eval(A); 
end proc:

です．

ソートでは配列の並べ替えをおこなうためにどうしても複雑なindexの動きをしますが，ゆっくり見ていけば理解できるはずです．たとえば

A:=Array([6,4,3,1,5,2]);
insertsort(A);

とした場合，

                     A := [6, 4, 3, 1, 2, 5]
                 "B", 2, 4, [6, 4, 3, 1, 2, 5]
                 "A", 2, 1, [4, 6, 3, 1, 2, 5]
                 "B", 3, 3, [4, 6, 3, 1, 2, 5]
                 "A", 3, 1, [3, 4, 6, 1, 2, 5]
                 "B", 4, 1, [3, 4, 6, 1, 2, 5]
                 "A", 4, 1, [1, 3, 4, 6, 2, 5]
                 "B", 5, 2, [1, 3, 4, 6, 2, 5]
                 "A", 5, 2, [1, 2, 3, 4, 6, 5]
                 "B", 6, 5, [1, 2, 3, 4, 6, 5]
                 "A", 6, 5, [1, 2, 3, 4, 5, 6]
                       [1, 2, 3, 4, 5, 6]

となります．挿入する前(Before)と後(After)の配列の違いを観察してください．たとえば，4番目まで終わった，

                 "B", 5, 2, [1, 3, 4, 6, 2, 5]

を考えます．5番目の要素の"2"が選ばれます(x:=A[i])．これを右側のもの(A[j])と順番に比べていきます．大きければ空いた席(A[j+1])と入れ替えます．

Compare出力
                 "C", 4, 6, [1, 3, 4, 6, _, 5]
                 "C", 3, 4, [1, 3, 4, _, 6, 5]
                 "C", 2, 3, [1, 3, _, 4, 6, 5]
                 "C", 1, 1, [1, _, 3, 4, 6, 5]

小さくなる(A[j] < x)かあるいはj=1までいけば比較は終了です．5番目の要素は1番目までいって，A[1] < xが成立して，A[2]に収まります．

課題1

上記の"C"以下が出力されるようにinsertsortを改良せよ．ただし下線"_"部には違う数字が入っている．その数字は？

ソートの視覚化

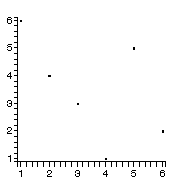
A:=Array([6,4,3,1,5,2]);
lA:=[seq([i,A[i]],i=1..6)];
pointplot(lA);

とすると

と表示されます．よこがindex，たてが入っている要素です．これを使って先程のinsertsortの途中経過を表示させます．

insertsort2:=proc(A::Array)
local n,x,i,j;
global tmp;
n:=op(ArrayDims(A))[2];
for i from 2 to n do
  x:=A[i];
  for j from i-1 to 1 by -1 do
  tmp:=[op(tmp),pointplot([seq([i,A[i]],i=1..n)])];
    if (A[j]<x) then break; end if;
    A[j+1]:=A[j];
  od;
  A[j+1]:=x;
od;
end proc:

tmp:=[]:
A:=Array([6,4,3,1,5,2]):
insertsort2(A):
tmp:=[op(tmp),pointplot([seq([i,A[i]],i=1..6)])]:
display(tmp,insequence=true);

課題2：選択ソートの作成

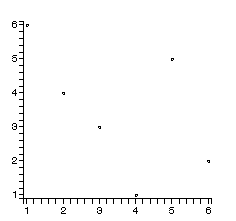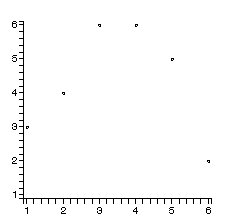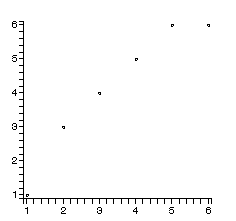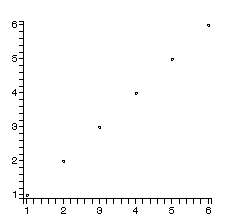
最も単純な選択ソートの以下の考え方にもとづいてスクリプトを書け．

選択ソート
まず，全体の中で最小のものを見つけ，それを先頭のA[1]と交換する．
次にA[2..n]の中で最小のものを見つけ，A[2]と交換する．
以下同様に続ける．

さらに，視覚化を試みよ．下のランダムな整数列の作成法を使って，大きめの数列を並べ替えた場合の挙動は次の通り．

tmp:=[];
A:=BigRandam(20);
selectsort2(A);
display(tmp,insequence=true,view=[0..21,0..21]);

ランダムな整数列の作成

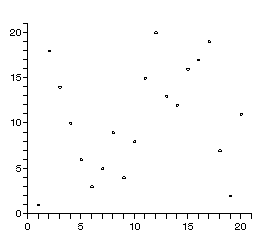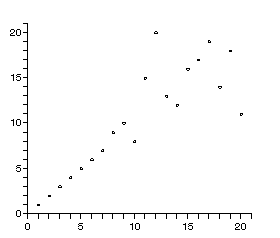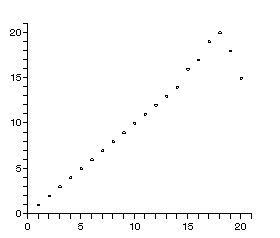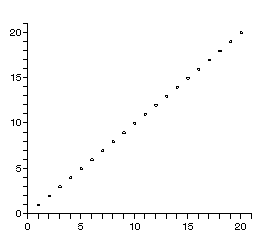
より要素数の大きなランダムな整数列を作成法の一つを以下に記す．

max_n:=20:
sel:=rand(1..max_n):
A:=Array([seq(i,i=1..max_n)]):
for k from 1 to 2*max_n do
  i:=sel();j:=sel();
  tmp:=A[i];A[i]:=A[j];A[j]:=tmp;
end do:

課題3

上の処理をprocに書き改めよ．入力は要素数，出力は数列が適当．

課題4:quick sort

上のinsertsortを参考にして，選んだ数より大きな数を右に，小さな数を左に置きかえる関数partition(A,first,last)を考えよ．選ぶ数としてはA[last]が簡単．これを使えば，quicksortは以下のようなスクリプトで書ける．

quicksort:=proc(A::Array,first::integer,last::integer)
local p;
if first<last then
  p:=partition(A,first,last);
  quicksort(A,first,p-1);
  quicksort(A,p+1,last);
end if:
eval(A);
end proc:

おなじみの視覚化ですが，pivotと呼ばれる数字を表示するように工夫してあります．

quicksort2:=proc(A::Array,first::integer,last::integer)
local p,title1;
global tmp;
if first<last then
  title1:=sprintf("%2d",A[last]);
  tmp:=[op(tmp),pointplot([seq([i,A[i]],i=1..n)],title=title1)];
  p:=partition(A,first,last);
  quicksort2(A,first,p-1);
  quicksort2(A,p+1,last);
end if:
eval(A);
end proc:

tmp:=[];n:=40:
A:=BigRandam(n):
quicksort2(A,1,n):
tmp:=[op(tmp),pointplot([seq([i,A[i]],i=1..n)],title="Finish")]:
display(tmp,insequence=true,view=[0..n+1,0..n+1]);