ハノイの塔(Towers of Hanoi)

数式処理演習　西谷　滋人

ハノイの塔

ハノイ(バラモン)の塔伝説

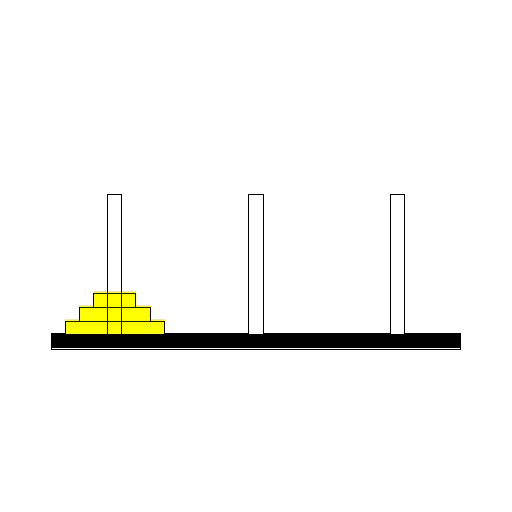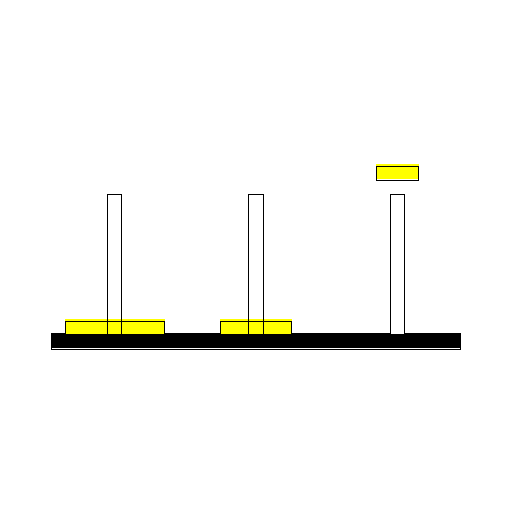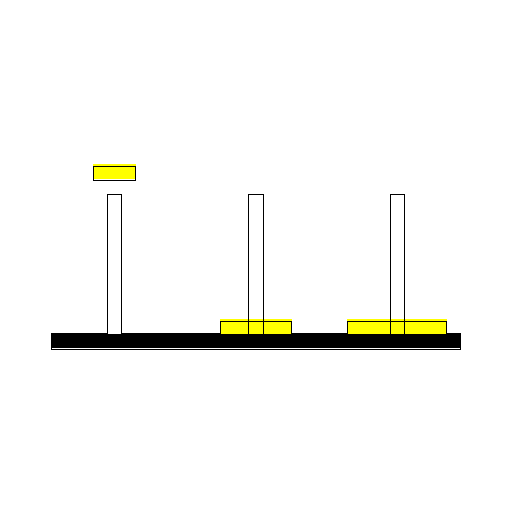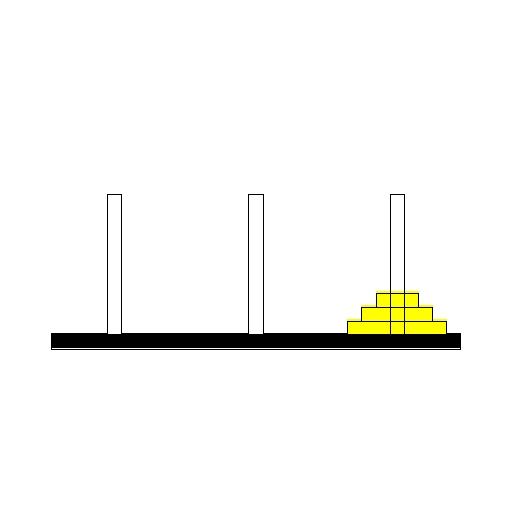
ベナレスにあるバラモン教の大寺院は世界の中心と記されており，そこに，針が３本立った真鍮製の板がある．神はその一本に64枚の純金の円盤をはめた．僧侶たちは昼夜の別なくそれを別の針に移し替える作業に専念している．そして移し替えが完了したとき，寺院もバラモン僧たちも崩壊し，この世が塵に帰るという。

『ハノイの塔』は1883年にフランスの数学者E.リュカ（Edouard Lucas）が考えたゲームです．リュカがこの物語を創作したのか，はたまたこの物語から発案したのかは不明．

ハノイの塔は次の通り：3本の棒があり，最初の棒には，おおきな円盤から小さな円盤が下から順に積まれて塔のようになっている．すべての円盤を最初の棒から最後の棒へ移し換えなさい．ただし，一度に一つの円盤しか動かせない．また，小さい円盤の上に大きな円盤を置いてはいけない．

手動版

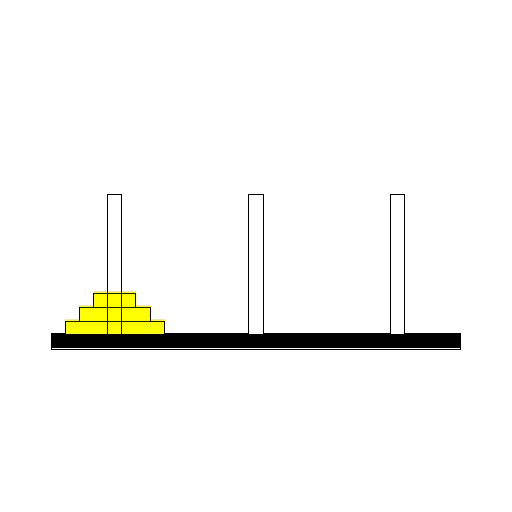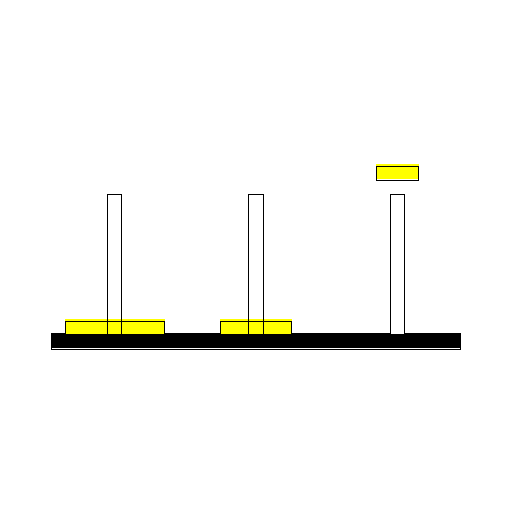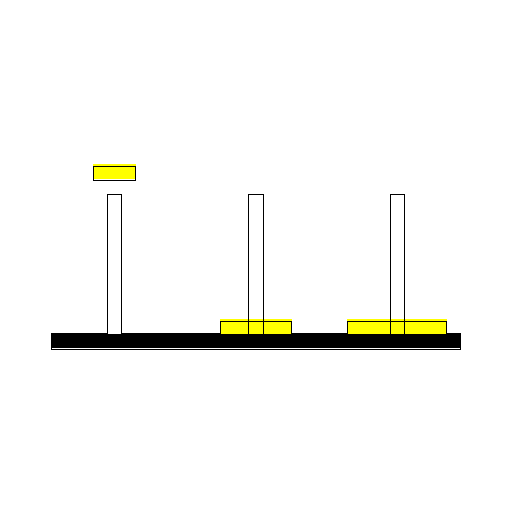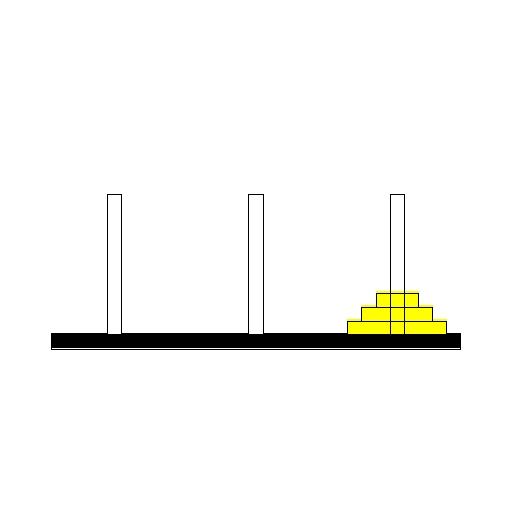
max_disk:=3;
ZeroArray(max_disk);
MoveList:=[[1,3],[1,2],[3,2],[1,3],[2,1],[2,3],[1,3]]:
n:=nops(MoveList):
for i from 1 to n do
  MakeMove(op(MoveList[i]));
end do:
print(peg);

自動版

max_disk:=4;
count:=0;
ZeroArray(max_disk);
PositionSmallest:=1;
MakeMove2(op(SmallestToWhere2(max_disk)));
while peg[3,max_disk]=0 do
  MakeMove2(op(DiskToWhere()));
  MakeMove2(op(SmallestToWhere2(max_disk)));
end do:
print("Congratulations!");

SmallestToWhereの例

SmallestToWhere2:=proc(n)
local from_peg,to_peg;
from_peg:=PositionSmallest;
if (n mod 2)=1 then
  to_peg:=PositionSmallest-1;
  if to_peg=0 then to_peg:=3; end if;
else
  to_peg:=PositionSmallest+1;
  if to_peg=4 then to_peg:=1; end if;
end if:
[from_peg,to_peg];
end proc:

R. Douglas Hofstadter. Metamagical themas. Scientific American, 248(2):16-22, March 1983.