Shift Scheduling Problem: L-Convex Minimization

We consider the shift scheduling problem in call centers [1]. Suppose a call center is operational during I=13 intervals. At the beginning of K=4 specified intervals, employees can start working, and each employee works for M=5 consecutive intervals. Shift k starts at the I_k-th interval and thus finishes at the beginning of interval I_k +M. We assume that I₁ = 1, I₂ = 3, I₃ = 6, I₄ = 9.

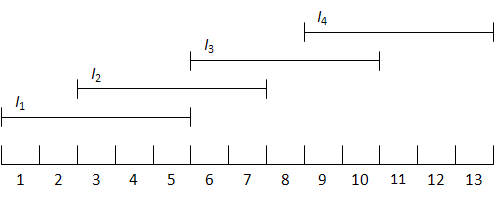
For each interval i (i=1, . . . , I) there is a function g_i representing the service level as a function of the number of employees working in that interval. Let y_k be the number of employees of shift k for k = 1, . . . ,K. Then the number of employees h_i(y) working at interval i is given by

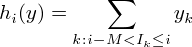
The value of g_i at this point is the attained service level in interval i. The overall service level is defined by

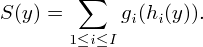
Now consider the following problem, which maximizes the service level for a given number of employees:

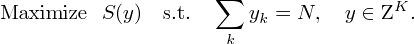
We assume that call arrivals are Poisson. The service criterion is the fraction of customers that has to wait longer than c seconds, e.g., c=11 seconds, before getting an operator, which should be below 5% in general. (We assume that no customers leave the system before getting an operator.)

Assuming that a statistical equilibrium is attained in each time interval, we use the formula for the stationary waiting time in an M|M|n queue as the service level. Let

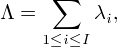
then the expected service level of an arbitrary customer under schedule y is equal to

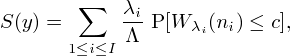
where and are the waiting time in an M|M|n queue with arrival rate and service rate . Thus we take

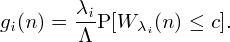
This function is indeed monotone increasing and concave for each i. Therefore, is multimodular. We can minimize by ODICON because multimodular functions and L-convex functions are equivalent objects that can be related through a simple coordinate transformation.

: Service criterion (We measure the fraction of customers that has to wait longer than seconds before getting an operator)

= (seconds)

: Service rate per hour

=
: Arrival rates per hour, 0 < ( = 1, 2, ... ,13)

	1	2	3	4	5	6	7	8	9	10	11	12	13
y1
y2
y3
y4

You can input parameters in the ranges 0 < c < 20 and , in the ranges 0 < , < 100.

You can also input an initial solution y. The input should satisfy > for all i. Then,

N = y₁+y₂+y₃+y₄ = .

(Note: "Reset" button resets your inputs to default values.)

This web application minimizes using ODICON .

---

[1] G. Koole and E. van der Sluis (2003): Optimal shift scheduling with a global service level constraint, IIE Transactions, Vol. 35, pp. 1049-1055.

---

Satoko Moriguchi, Nobuyuki Tsuchimura