巡回セールスマン問題

西谷　滋人

理論

巡回セールスマン問題とは，ある街から出発していくつかの街を次々とめぐって元の街に戻ってくる最短の経路を求める問題です．訪れる街の数が少ないときにはすべての経路を数え上げればいいのですが，数が増えるとその計算時間は指数関数的に増えてしまうと予想される問題です．このような問題はセールスマンだけでなく，コンピュータのCPUの配置や，都市ガスの配管設計などでも出会う問題です．

対象となる経路の長さの合計を

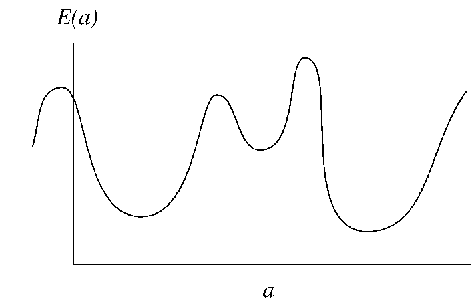
としておきます．ここでa はそれぞれの街の順番あるいは配置を示しています．r はそれぞれ街の座標で||r ||で距離を求めます．するとこの関数は模式的に図のようになると考えることができます．すべての配置についてE(a) を求めれば，最小値が求まります．あるいは初期の配置を

a = [1,2,3,...,N,1]

として，一定の手順で変更δa を加え，E(a +δa) が下がった場合にその配置を採用するという方法をとることも出来ます．しかし，この方法は極小値に落ちてしまうことが分かるでしょう．最小値を探すには時として坂を駆け登る必要があるのです．このような問題の一つの解法としてアニーリング法(simulated annealing)があります．これは格子欠陥を多く含んだ金属を高温へ上げて欠陥を掃き出し柔らかくする熱処理(焼きなまし，annealing)からの類推で名付けられた手法です．

$配置${\bf a}$とその経路の総和$E({\bf a})$を示す模式図$

アルゴリズム

アルゴリズムは以下のとおりです．

配置aを仮定しE(a)を求める．
aからすこし違った配置a+δa を作る．
Δ E = E(a+δa)-E(a) を求める．
Δ E < 0 なら新たな配置を採用する．
Δ E > 0 なら新たな配置をexp(-Δ E/T) の確率で受け入れる．
手順2以下を適当な回数繰り返す．

ここでT は温度から類推される制御パラメータで，十分大きい場合はすべての状態が採用されます．一方，Tを下げるにつれて採用される試行が少なくなり，徐々に状態が凍結されていきます．a+δa の生成方法とT の下げ方をうまく取れば最小値に近い状態が確率的に高く出現し，最小値かそれに近い状態へ落ち着くというアルゴリズムです．

計算例

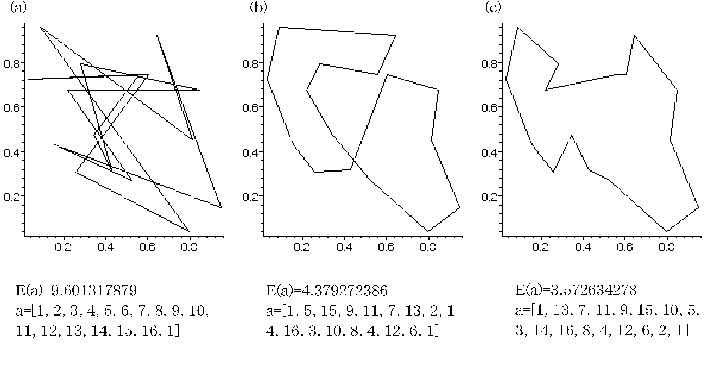
ランダムに生成した16個の街に適用した巡回セールスマン問題の(a)初期配置，(b)単純にE(a)が下がった場合だけを採用した結果，および(c) simulated annealingの計算結果．

Maple script

以下は街の位置をランダムに生成し表示するMaple scriptです．

salesman.mws

    restart;
    with(plots):
    N_city:=16;
    Path:=[seq(i,i=1..N_city),1];
    Position:=seq([evalf(rand()/10^12),evalf(rand()/10^12)],i=1..N_city):
    Real_Path:=[seq(Position[Path[i]],i=1..N_city),Position[1]]:
    PLOT(CURVES(Real_Path));

問題とヒント

街の間の距離をあらかじめ計算して，2次元の配列に入れておき，配置a から任意に2都市を取りだして入れ替える試行をδa として上述のアルゴリズムにしたがって最短経路を探すプログラムを作成してください．

試行にともなうトータル距離の変化．
初期状態と最終状態のパス

を書かせてみてください．

ヒント:2..N_cityの整数をランダムに生成する関数

    sel_city:=rand(2..N_city):

参考文献

“計算物理学入門”Harvey Gould and Jan Tobochnik著，鈴木増雄監訳，溜渕継博監翻訳，石川正勝，宮島佐介訳(ピアソン・エデュケーション，2000)．